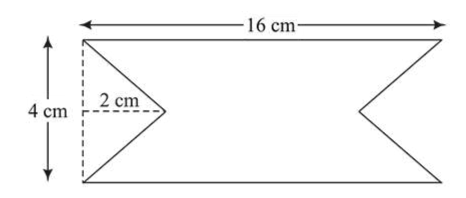
At time t=0 magnetic field of 1000 Gauss is passing perpendicularly through the area defined

(1) According to question, $d B=1000-500=500$ gauss

$=500 \times 10^{-4} \mathrm{~T}$

Time $d t=5 \mathrm{~s}$

Using faraday law

Induced $E M F, e=\left|-\frac{d \phi}{d t}\right|=\left|A \frac{d B}{d t}\right|$

$\frac{d B}{d t}=\frac{1000-500}{5} \times 10^{-4}=10^{-2} \mathrm{~T} / \mathrm{sec}$

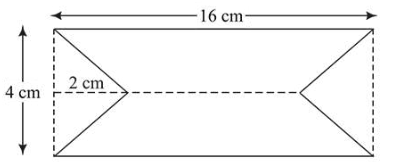
Area, $A=$ ar of $\square-2$ ar of $\Delta=(16 \times 4-2 \times$ Area of triangle) $\mathrm{cm}^{2}$

$=\left(64-2 \times \frac{1}{2} \times 2 \times 4\right) \mathrm{cm}^{2}$

$=56 \times 10^{-4} \mathrm{~m}^{2}$

$\therefore \varepsilon_{\text {induced }}=\left|A \frac{d B}{d t}\right|=56 \times 10^{-4} \times 10^{-2}=56 \times 10^{-6} \mathrm{~V}=56 \mu \mathrm{V}$