At what angle should a ray of light be incident on the face

The incident, refracted, and emergent rays associated with a glass prism ABC are shown in the given figure.

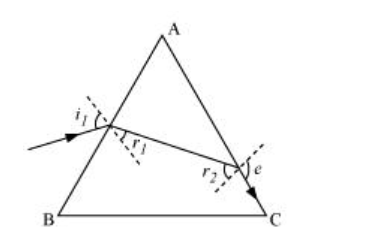
Angle of prism, ∠A = 60°

Refractive index of the prism, µ = 1.524

$i_{1}=$ Incident angle

$r_{1}=$ Refracted angle

$r_{2}=$ Angle of incidence at the face $\mathrm{AC}$

e = Emergent angle = 90°

According to Snell’s law, for face AC, we can have:

$\frac{\sin e}{\sin r_{2}}=\mu$

$\sin r_{2}=\frac{1}{\mu} \times \sin 90^{\circ}$

$=\frac{1}{1.524}=0.6562$

$\therefore r_{2}=\sin ^{-1} 0.6562 \approx 41^{\circ}$

It is clear from the figure that angle $A=r_{1}+r_{2}$

$\therefore r_{1}=A-r_{2}=60-41=19^{\circ}$

According to Snell’s law, we have the relation:

$\mu=\frac{\sin i_{1}}{\sin r_{1}}$

$\sin i_{1}=\mu \sin r_{1}$

$=1.524 \times \sin 19^{\circ}=0.496$

$\therefore i_{1}=29.75^{\circ}$

Hence, the angle of incidence is 29.75°.