Balance the following equations in basic medium by ion-electron method and oxidation

Solution:

(a)

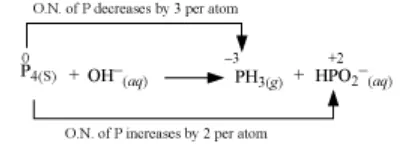
The O.N. (oxidation number) of $\mathrm{P}$ decreases from 0 in $\mathrm{P}_{4}$ to $-3$ in $\mathrm{PH}_{3}$ and increases from 0 in $\mathrm{P}_{4}$ to $+2$ in $\mathrm{HPO}_{2}^{-}$. Hence, $\mathrm{P}_{4}$ acts both as an oxidizing agent and a reducing agent in this reaction.

Ion–electron method:

The oxidation half equation is:

$\mathrm{P}_{4}(\mathrm{~s}) \rightarrow \mathrm{HPO}_{2}^{-}(\mathrm{aq})$

The P atom is balanced as:

$\mathrm{P}_{4}(\mathrm{~s}) \rightarrow 4 \mathrm{HPO}_{2}^{-}(\mathrm{aq})$

The O atom is balanced by adding 8 H2O molecules:

$\mathrm{P}_{4}(\mathrm{~s})+8 \mathrm{H}_{2} \mathrm{O} \rightarrow 4 \mathrm{HPO}_{2}^{-}(\mathrm{aq})$

The H atom is balanced by adding 12 H+ ions:

$\mathrm{P}_{4}(\mathrm{~s})+8 \mathrm{H}_{2} \mathrm{O} \rightarrow 4 \mathrm{HPO}_{2}^{-}(\mathrm{aq})+12 \mathrm{H}^{+}$

The charge is balanced by adding e– as:

$\mathrm{P}_{4}(\mathrm{~s})+8 \mathrm{H}_{2} \mathrm{O} \rightarrow 4 \mathrm{HPO}_{2}^{-}(\mathrm{aq})+12 \mathrm{H}^{+}+8 \mathrm{e}^{-} \quad \ldots$ (i)

The reduction half equation is:

$\mathrm{P}_{4(s)} \longrightarrow \mathrm{PH}_{3(g)}$

The P atom is balanced as:

$\mathrm{P}_{4}(\mathrm{~s}) \rightarrow 4 \mathrm{PH}_{3}(\mathrm{~g})$

The H is balanced by adding 12 H+ as:

$\mathrm{P}_{4}(\mathrm{~s})+12 \mathrm{H}^{+} \rightarrow 4 \mathrm{PH}_{3}(\mathrm{~g})$

The charge is balanced by adding 12e– as:

$\mathrm{P}_{4}(\mathrm{~s})+12 \mathrm{H}^{+}+12 \mathrm{e}^{-} \rightarrow 4 \mathrm{PH}_{3}(\mathrm{~g})$

By multiplying equation (i) with 3 and (ii) with 2 and then adding them, the balanced chemical equation can be obtained as:

$5 \mathrm{P}_{4}(\mathrm{~s})+24 \mathrm{H}_{2} \mathrm{O} \rightarrow 12 \mathrm{HPO}_{2}^{-}+8 \mathrm{PH}_{3}(\mathrm{~g})+12 \mathrm{H}^{+}$

As, the medium is basic, add 12OH– both sides as:

$5 \mathrm{P}_{4}(\mathrm{~s})+12 \mathrm{H}_{2} \mathrm{O}+12 \mathrm{OH}^{-} \rightarrow 12 \mathrm{HPO}_{2}^{-}+8 \mathrm{PH}_{3}(\mathrm{~g})$

This is the required balanced equation.

Oxidation number method:

Let, total no of P reduced = x

∴">∴∴ Total no of P oxidised = 4 – x

$\mathrm{P}_{4}(\mathrm{~s})+\mathrm{OH}^{-} \rightarrow x \mathrm{PH}_{3}(\mathrm{~g})+(4-x) \mathrm{HPO}_{2}^{-}$

Total decrease in oxidation number of P = x × 3 = 3x

Total increase in oxidation number of $P=(4-x) \times 2=8-2 x$

$\because 3 x=8-2 x$

$x=8 / 5$

From (i),

$5 \mathrm{P}_{4}(\mathrm{~s})+5 \mathrm{OH}^{-} \rightarrow 8 \mathrm{PH}_{3}(\mathrm{~g})+12 \mathrm{HPO}_{2}^{-}$

Since, reaction occures in basic medium, the charge is balanced by adding 7OH– on LHS as:

$5 \mathrm{P}_{4}(\mathrm{~s})+12 \mathrm{OH}^{-} \rightarrow 8 \mathrm{PH}_{3}(\mathrm{~g})+12 \mathrm{HPO}_{2}^{-}$

The $\mathrm{O}$ atoms are balanced by adding $12 \mathrm{H}_{2} \mathrm{O}$ as:

$5 \mathrm{P}_{4}(\mathrm{~s})+12 \mathrm{H}_{2} \mathrm{O}+12 \mathrm{OH}^{-} \rightarrow+12 \mathrm{HPO}_{2}^{-}+8 \mathrm{PH}_{3}(\mathrm{~g})$

This is the required balanced equation.

(b)

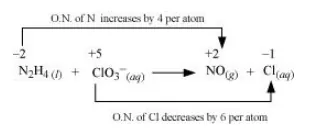
The oxidation number of $\mathrm{N}$ increases from $-2$ in $\mathrm{N}_{2} \mathrm{H}_{4}$ to $+2$ in $\mathrm{NO}$ and the oxidation number of $\mathrm{Cl}$ decreases from $+5$ in $\mathrm{ClO}_{3}^{-}$to $-1$ in $\mathrm{Cl}^{-}$. Hence, in this

reaction, $\mathrm{N}_{2} \mathrm{H}_{4}$ is the reducing agent and $\mathrm{ClO}_{3}^{-}$is the oxidizing agent.

Ion–electron method:

The oxidation half equation is:

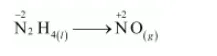
The N atoms are balanced as:

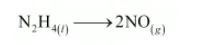
The oxidation number is balanced by adding 8 electrons as:

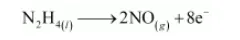
The charge is balanced by adding 8 OH–ions as:

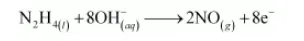
The O atoms are balanced by adding 6H2O as:

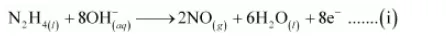
The reduction half equation is:

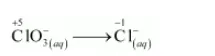
The oxidation number is balanced by adding 6 electrons as:

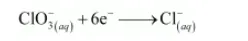
The charge is balanced by adding 6OH– ions as:

The O atoms are balanced by adding 3H2O as:

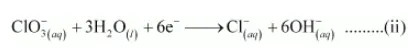
The balanced equation can be obtained by multiplying equation (i) with 3 and equation (ii) with 4 and then adding them as:

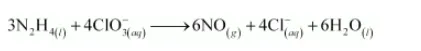
Oxidation number method:

Total decrease in oxidation number of N = 2 × 4 = 8

 

Total increase in oxidation number of Cl = 1 × 6 = 6

On multiplying $\mathrm{N}_{2} \mathrm{H}_{4}$ with 3 and $\mathrm{ClO}_{3}^{-}$with 4 to balance the increase and decrease in $\mathrm{O} . \mathrm{N}$., we get:

The N and Cl atoms are balanced as:

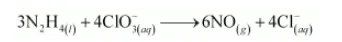
The O atoms are balanced by adding 6H2O as:

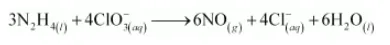
This is the required balanced equation.

(c)

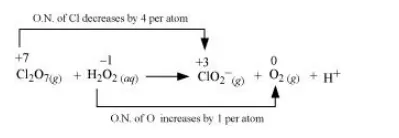
The oxidation number of $\mathrm{Cl}$ decreases from $+7$ in $\mathrm{Cl}_{2} \mathrm{O}_{7}$ to $+3$ in $\mathrm{ClO}_{2}^{-}$and the oxidation number of $\mathrm{O}$ increases from $-1$ in $\mathrm{H}_{2} \mathrm{O}_{2}$ to zero in $\mathrm{O}_{2}$. Hence, in this

Ion–electron method:

The oxidation half equation is:

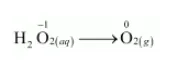
The oxidation number is balanced by adding 2 electrons as:

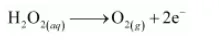
The charge is balanced by adding 2OH–ions as:

The oxygen atoms are balanced by adding 2H2O as:

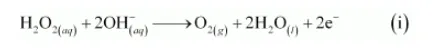
The reduction half equation is:

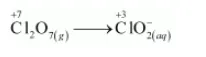
The Cl atoms are balanced as:

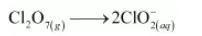
The oxidation number is balanced by adding 8 electrons as:

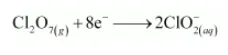
The charge is balanced by adding 6OH– as:

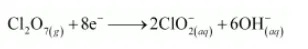
The oxygen atoms are balanced by adding 3H2O as:

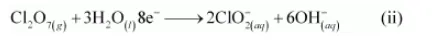
The balanced equation can be obtained by multiplying equation (i) with 4 and adding equation (ii) to it as:

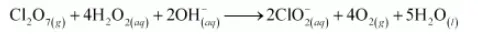
Oxidation number method:

Total decrease in oxidation number of $\mathrm{Cl}_{2} \mathrm{O}_{7}=4 \times 2=8$

Total increase in oxidation number of $\mathrm{H}_{2} \mathrm{O}_{2}=2 \times 1=2$

 

By multiplying H2O2 and O2 with 4 to balance the increase and decrease in the oxidation number, we get:

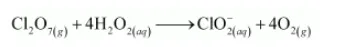
The Cl atoms are balanced as:

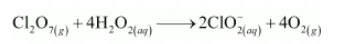
The O atoms are balanced by adding 3H2O as:

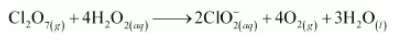
The H atoms are balanced by adding 2OH– and 2H2O as:

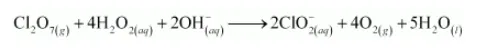
This is the required balanced equation.