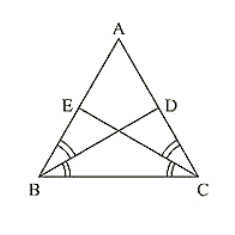
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC

Given that ΔABC is isosceles with AB = AC and BD and CE are bisectors of ∠B and ∠ C We have to prove BD = CE

Since AB = AC

⟹ ΔABC = ΔACB ... (i)

[Angles opposite to equal sides are equal]

Since BD and CE are bisectors of ∠B and ∠C

∠ABD = ∠DBC = ∠BCE = ECA = ∠B/2 = ∠C/2

Now,

Consider ΔEBC = ΔDCB

∠EBC = ∠DCB [∠B = ∠C] [From (i)]

BC = BC [Common side]

∠BCE = ∠CBD [From (ii)]

So, by ASA congruence criterion, we have Δ EBC ≅ Δ DCB

Now,

CE = BD [Corresponding parts of congruent triangles we equal]

or, BD = CE

Hence proved

Since AD ∥ BC and transversal AB cuts at A and B respectively

∠DAO = ∠OBC .... (ii) [alternate angle]

And similarly AD ∥ BC and transversal DC cuts at D and C respectively

∠ADO = ∠OBC   …. (iii) [alternate angle]

Since AB end CD intersect at O.

∠AOD = ∠BOC    [Vertically opposite angles]

Now consider ΔAOD and ΔBOD

∠DAO = ∠OBC [From (ii)]

AD = BC   [From (i)]

And ∠ADO = ∠OCB  [From (iii)]

So, by ASA congruence criterion, we have

ΔAOD ≅ ΔBOC

Now,

AO = OB and DO = OC [Corresponding parts of congruent triangles are equal)

Lines AB and CD bisect at O.

Hence proved