Bisectors of the angles B and C

Given Lines, $O B$ and $O C$ are the anqle bisectors of $\angle B$ and $\angle C$ of an isosceles $\triangle A B C$ such

that $A B=A C$ which intersect each other at $O$ and $B O$ is produced to $M$.

To prove   $\angle M O C=\angle A B C$.

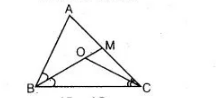
Proof $\ln \triangle A B C$, $A B=A C$[given]

$\Rightarrow$ $\angle A C B=\angle A B C$ [angles opposite to equal sides are equal]

$\frac{1}{2} \angle A C B=\frac{1}{2} \angle A B C$ [dividing both sides by 2]

$\Rightarrow$ $\angle O C B=\angle O B C$ $\ldots($ i)

[since, $O B$ and $O C$ are the bisector of $\angle B$ and $\angle C$ ]

Now,   $\angle M O C=\angle O B C+\angle O C B$

[exterior angle of a triangle is equal to the sum of two interior angles]

$\Rightarrow$ $\angle M O C=\angle O B C+\angle O B C$ [from Eq. (i)]

$\Rightarrow$ $\angle M O C=2 \angle O B C$

$\Rightarrow$ $\angle M O C=\angle A B C$[since, $O B$ is the bisector of $\angle B$ ]

Hence proved.