Question:
Box A contains 25 slips of which 19 are marked ₹ 1 and other are marked ₹ 5 each. Box B contains 50 slips of which 45 are marked ₹ 1 each and
others are marked ₹ 13 each. Slips of both boxes are poured into a third box and resuffled. A slip is drawn at random. What is the probability that it is
marked other than ₹ 1?
Solution:
Total number of slips in a box, n(S) = 25 + 50 = 75
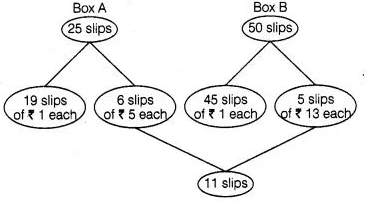
Erom the chart it is clear that, there are 11 slips which are marked other than $₹ 1$.
$\therefore \quad$ Required probability $=\frac{\text { Number of slips other than } ₹ 1}{\text { Total number of slips }}=\frac{11}{75}$