Calculate potential on the axis of a disc

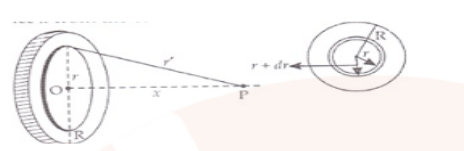
In the above figure, we can see that the disc is divided into several charged rings. Let P be the point on the axis of the disc at a distance x from the centre of the disc.

The radius of the ring is r and the width is dr. dq is the charge on the ring which is given as

dq = σdA = σ2πrdr

The potential is given as

$d V=\frac{1}{4 \pi \epsilon_{0}} \frac{d q}{\sqrt{r^{2}+x^{2}}}=\frac{1}{4 \pi \epsilon_{0}} \frac{(\sigma 2 \pi r d r)}{\sqrt{r^{2}+x^{2}}}$

The total potential at P is given as

Q/2πε0R2 (√R2 + x2 –x)