Calculate the degree of ionization of $0.05 \mathrm{M}$ acetic acid if its $\mathrm{pK}_{\mathrm{a}}$ value is $4.74$.
How is the degree of dissociation affected when its solution also contains (a) $0.01 \mathrm{M}$ (b) $0.1 \mathrm{M}$ in $\mathrm{HCl}$ ?
$c=0.05 \mathrm{M}$
$p K_{a}=4.74$
$p K_{a}=-\log \left(K_{a}\right)$
$K_{a}=1.82 \times 10^{-5}$
$K_{a}=c \alpha^{2} \quad \alpha=\sqrt{\frac{K_{a}}{c}}$
$\alpha=\sqrt{\frac{1.82 \times 10^{-5}}{5 \times 10^{-2}}}=1.908 \times 10^{-2}$
When $\mathrm{HCl}$ is added to the solution, the concentration of $\mathrm{H}^{+}$ions will increase. Therefore, the equilibrium will shift in the backward direction i.e., dissociation of acetic acid will decrease.
Case I: When 0.01 M HCl is taken.
Let x be the amount of acetic acid dissociated after the addition of HCl.
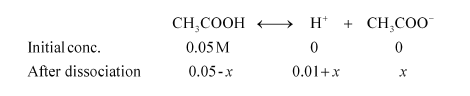
As the dissociation of a very small amount of acetic acid will take place, the values i.e., 0.05 – x and 0.01 + x can be taken as 0.05 and 0.01 respectively
$K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}$
$\therefore K_{a}=\frac{(0.01) x}{0.05}$
$x=\frac{1.82 \times 10^{-5} \times 0.05}{0.01}$
$x=1.82 \times 10^{-3} \times 0.05 \mathrm{M}$
Now,
$\alpha=\frac{\text { Amount of acid dissociated }}{\text { Amount of acid taken }}$
$=\frac{1.82 \times 10^{-3} \times 0.05}{0.05}$
$=1.82 \times 10^{-3}$
Case II: When 0.1 M HCl is taken.
Let the amount of acetic acid dissociated in this case be X. As we have done in the first case, the concentrations of various species involved in the reaction are:
