Calculate the standard cell potentials of galvanic cells in which the following reactions take place:

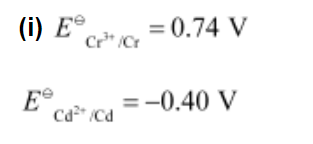
The galvanic cell of the given reaction is depicted as:

$\mathrm{Cr}_{(s)}\left|\mathrm{Cr}^{3+}{ }_{(a q)}\right|\left|\mathrm{Cd}^{2+}{ }_{(a q)}\right| \mathrm{Cd}_{(s)}$

Now, the standard cell potential is

$E_{\text {cell }}^{\ominus}=E_{\mathrm{R}}^{\ominus}-E_{\mathrm{L}}^{\ominus}$

$=-0.40-(-0.74)$

$=+0.34 \mathrm{~V}$

$\Delta_{\mathrm{r}} G^{\ominus}=-n \mathrm{~F} E_{\text {cell }}^{\ominus}$

In the given equation,

n = 6

F = 96487 C mol−1

$E_{\text {cell }}^{\ominus}=+0.34 \mathrm{~V}$

Then, $\Delta_{\mathrm{r}} G^{\ominus}=-6 \times 96487 \mathrm{C} \mathrm{mol}^{-1} \times 0.34 \mathrm{~V}$

= −196833.48 CV mol−1

= −196833.48 J mol−1

= −196.83 kJ mol−1

Again,

$\Delta_{\mathrm{r}} G^{\ominus}=-\mathrm{R} T \ln K$

$\Rightarrow \Delta_{\mathrm{r}} G^{\ominus}=-2.303 \mathrm{R} T \ln K$

$\Rightarrow \log K=-\frac{\Delta_{\mathrm{r}} G}{2.303 \mathrm{R} T}$

$=\frac{-196.83 \times 10^{3}}{2.303 \times 8.314 \times 298}$

= 34.496

$\therefore \mathrm{K}=$ antilog $(34.496)$

= 3.13 × 1034

(ii) $E_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{\ominus}=0.77 \mathrm{~V}$

$E_{\mathrm{Ag}^{+} / \mathrm{Ag}}=0.80 \mathrm{~V}$

The galvanic cell of the given reaction is depicted as:

$\mathrm{Fe}^{2+}{ }_{(a q)}\left|\mathrm{Fe}^{3+}(a q) \| \mathrm{Ag}^{+}{ }_{(a q)}\right| \mathrm{Ag}_{(s)}$

Now, the standard cell potential is

$E_{\text {cell }}^{\ominus}=E_{\mathrm{R}}^{\ominus}-E_{\mathrm{L}}^{\ominus}$

$=0.80-0.77$

$=0.03 \mathrm{~V}$

Here, n = 1.

Then, $\Delta_{\mathrm{r}} G^{\ominus}=-n \mathrm{~F} E_{\text {cell }}^{\ominus}$

= −1 × 96487 C mol−1 × 0.03 V

= −2894.61 J mol−1

= −2.89 kJ mol−1

Again, $\Delta_{\mathrm{r}} G^{\ominus}=-2.303 \mathrm{R} T \ln K$

$\Rightarrow \log K=-\frac{\Delta_{\mathrm{r}} G}{2.303 \mathrm{R} T}$

$=\frac{-2894.61}{2.303 \times 8.314 \times 298}$

= 0.5073

$\therefore \mathrm{K}=$ antilog $(0.5073)$

= 3.2 (approximately)