Choose the correct answer of the following question:

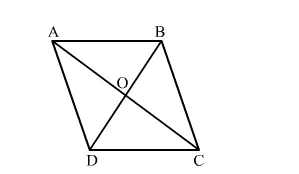
We have,

$\mathrm{BD}=20 \mathrm{~cm}$

$\Rightarrow \mathrm{BO}=\frac{\mathrm{BD}}{2}=\frac{20}{2}=10 \mathrm{~cm}$

As, area of the rhombus $A B C D=480 \mathrm{~cm}^{2}$

$\Rightarrow \frac{1}{2} \times \mathrm{AC} \times \mathrm{BD}=480$

$\Rightarrow \frac{1}{2} \times \mathrm{AC} \times 20=480$

$\Rightarrow \mathrm{AC} \times 10=480$

$\Rightarrow \mathrm{AC}=\frac{480}{10}$

$\Rightarrow \mathrm{AC}=48 \mathrm{~cm}$

$\Rightarrow \mathrm{AO}=\frac{\mathrm{AC}}{2}=\frac{48}{2}=24 \mathrm{~cm}$

Now, in $\triangle \mathrm{AOB}$,

Using Pythagoras theorem,

$\mathrm{AB}^{2}=\mathrm{AO}^{2}+\mathrm{BO}^{2}$

$=24^{2}+10^{2}$

$=576+100$

$\Rightarrow \mathrm{AB}^{2}=676$

$\Rightarrow \mathrm{AB}=\sqrt{676}$

$\therefore \mathrm{AB}=26 \mathrm{~cm}$

Hence, the correct answer is option (c).