Choose the correct answer of the following question:

Solution:

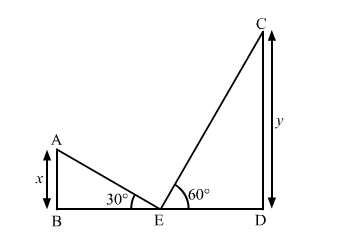
Let AB and CD be the two towers such that AB = x and CD = y.

We have,

$\angle \mathrm{AEB}=30^{\circ}, \angle \mathrm{CED}=60^{\circ}$ and $\mathrm{BE}=\mathrm{DE}$

In $\Delta \mathrm{ABE}$,

$\tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{BE}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{x}{\mathrm{BE}}$

$\Rightarrow \mathrm{BE}=x \sqrt{3}$

Also, in $\Delta \mathrm{CDE}$,

$\tan 60^{\circ}=\frac{\mathrm{CD}}{\mathrm{DE}}$

$\Rightarrow \sqrt{3}=\frac{y}{\mathrm{DE}}$

$\Rightarrow \mathrm{DE}=\frac{y}{\sqrt{3}}$

As, BE $=\mathrm{DE}$

$\Rightarrow x \sqrt{3}=\frac{y}{\sqrt{3}}$

$\Rightarrow \frac{x}{y}=\frac{1}{\sqrt{3} \times \sqrt{3}}$

$\Rightarrow \frac{x}{y}=\frac{1}{3}$

$\therefore x: y=1: 3$

Hence, the correct answer is option (c).