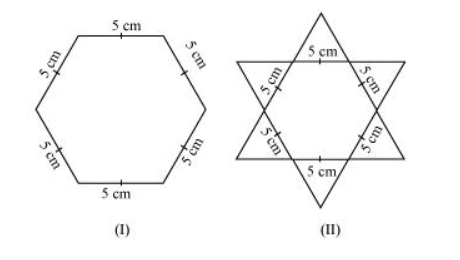
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Solution:

It can be observed that hexagonal-shaped rangoli has 6 equilateral triangles in it.



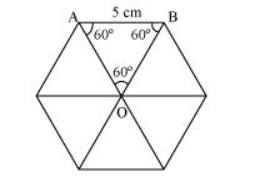
Area of $\Delta \mathrm{OAB}=\frac{\sqrt{3}}{4}(\text { side })^{2}=\frac{\sqrt{3}}{4}(5)^{2}$

$=\frac{\sqrt{3}}{4}(25)=\frac{25 \sqrt{3}}{4} \mathrm{~cm}^{2}$

Area of hexagonal-shaped rangoli $=6 \times \frac{25 \sqrt{3}}{4}=\frac{75 \sqrt{3}}{2} \mathrm{~cm}^{2}$

Area of equilateral triangle having its side as $1 \mathrm{~cm}=\frac{\sqrt{3}}{4}(1)^{2}=\frac{\sqrt{3}}{4} \mathrm{~cm}^{2}$

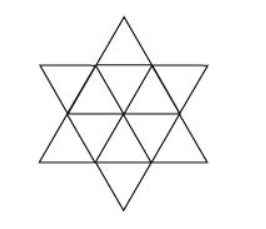
Number of equilateral triangles of $1 \mathrm{~cm}$ side that can be filled

in this hexagonal-shaped rangoli $=\frac{\frac{75 \sqrt{3}}{2}}{\frac{\sqrt{3}}{4}}=150$

Star-shaped rangoli has 12 equilateral triangles of side $5 \mathrm{~cm}$ in it.



Area of star-shaped rangoli $=12 \times \frac{\sqrt{3}}{4} \times(5)^{2}=75 \sqrt{3}$

Number of equilateral triangles of $1 \mathrm{~cm}$ side that can be filled

in this star-shaped rangoli $=\frac{75 \sqrt{3}}{\frac{\sqrt{3}}{4}}=300$

Therefore, star-shaped rangoli has more equilateral triangles in it.