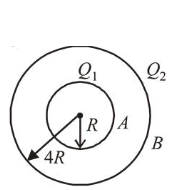
Concentric metallic hollow spheres of radii $R$ and $4 R$ hold charges $Q_{1}$ and $Q_{2}$ respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference $V(R)-V(4 R)$ is :
Correct Option: 1
(1) We have given two metallic hollow spheres of radii $R$ and $4 R$ having charges $Q_{1}$ and $Q_{2}$ respectively.
Potential on the surface of inner sphere (at $A$ )
$V_{A}=\frac{k Q_{1}}{R}+\frac{k Q_{2}}{4 R}$
Potential on the surface of outer sphere (at $B$ )
$V_{B}=\frac{k Q_{1}}{4 R}+\frac{k Q_{2}}{4 R}$ $\left(\right.$ Here, $\left.k=\frac{1}{4 \pi \varepsilon_{0}}\right)$
Potential difference,
$\Delta V=V_{A}-V_{B}=\frac{3}{4} \cdot \frac{k Q_{1}}{R}=\frac{3}{16 \pi \in_{0}} \cdot \frac{Q_{1}}{R}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
