Question:
Consider a badminton racket with length scales as shown in the figure.
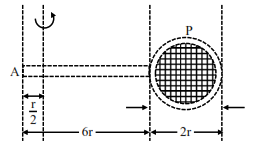
If the mass of the linear and circular portions of the badminton racket are same (M) and the mass of the threads are negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, $\frac{r}{2}$ distance from the end $\mathrm{A}$ of the handle will be ........ $\mathrm{Mr}^{2}$.
Solution:
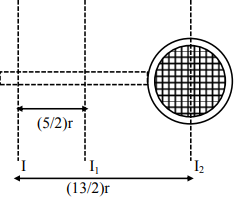
$I=\left[I_{1}+M\left(\frac{5}{2} r\right)^{2}\right]+\left[I_{2}+M\left(\frac{13 r}{2}\right)^{2}\right]$
$=\left[\frac{\mathrm{M}\left(36 \mathrm{r}^{2}\right)}{12}+\frac{\mathrm{M}\left(25 \mathrm{r}^{2}\right)}{4}\right]+\left[\frac{\mathrm{Mr}^{2}}{2}+\frac{169 \mathrm{Mr}^{2}}{4}\right]$
=52 \mathrm{Mr}^{2}
Ans. $52.00$