Question:
Consider a rectangle ABCD having $5,7,6,9$ points in the interior of the line segments $\mathrm{AB}$, $\mathrm{CD}, \mathrm{BC}, \mathrm{DA}$
respectively. Let $\alpha$ be the number of triangles having these points from different sides as vertices and $\beta$ be the number of quadrilaterals
having these points from different sides as vertices. Then $(\beta-\alpha)$ is equal to :
Correct Option: , 4
Solution:
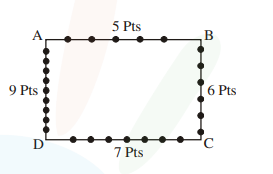
$\alpha=$ Number of triangles
$\alpha=5 \cdot 6 \cdot 7+5 \cdot 7 \cdot 9+5 \cdot 6 \cdot 9+6 \cdot 7 \cdot 9$
$=210+315+270+378$
$=1173$
$\beta=$ Number of Quadrilateral
$\beta=5 \cdot 6 \cdot 7 \cdot 9=1890$
$\beta-\alpha=1890-1173=717$