Consider that a d^6 metal ion M^2+ forms a complex with aqua ligands,

If spin only magnetic moment of the complex is $4.90 \mathrm{BM}$, it means number of unpaired electrons should be 4 .

(A) In octahedral complex: $\left[\mathrm{M}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}$

$d^{6}$

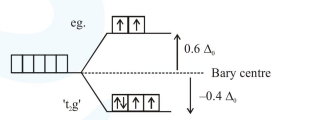
$\begin{aligned} \text { C.F.S.E. } &=\left(-0.4 \Delta_{0}\right) \times 4+\left(+0.6 \Delta_{0}\right) \times 2+0 \times \mathrm{P} \\ &=-0.4 \Delta_{0} \end{aligned}$

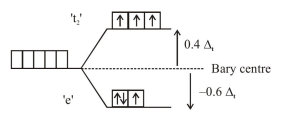
$\begin{aligned} \text { C.F.S.E. } &=\left(-0.6 \Delta_{t}\right) \times 3+\left(+0.4 \Delta_{t}\right) \times 3+0 \times \mathrm{P} \\ &=-0.6 \Delta_{t} \end{aligned}$