Consider the function $\mathrm{f}: \mathbf{R} \rightarrow \mathbf{R}$, defined by
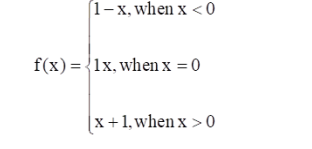
Write its domain and range. Also, draw the graph of f(x).
Given:
f(x)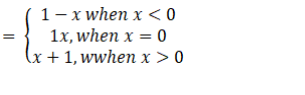 
To Find:
Domain and Range of $\mathrm{f}(\mathrm{x})$
When $f(x)=1-x \mid x<0$
In this case there is no value of $x(x<0)$ which makes the above expression undefined.
Therefore
Domain(f) $=(-\infty, 0) \ldots(1)$
When f(x) = x | x = 0
In this case there is no value other than 0 which makes the above expression undefined.
Therefore
Domain(f) $=0 \ldots(2)$
When f(x) = x + 1 | x > 0
In this case there is no value of x (x > 0) which makes the above expression undefined.
Therefore,
Domain(f) $=(0, \infty) \ldots(3)$
From equations (1),(2) \& (3) We can say that the domain of $f(x)$ as a whole :
Domain $(f)=(-\infty, \infty)$
Now when, $f(x)=1-x$
$x=1-f(x)$
As $x$ ranges from $-\infty$ to 0 , then $f(x)$ ranges from 1 to $\infty$
Therefore,
Range $(f)=(1, \infty) \ldots(4)$
Now when, $f(x)=x$
As x = 0
Therefore,
Range(f) = 0 …(5)
Now when, f(x) = x +1
$x=f(x)-1$
As $x$ ranges from 0 to $\infty$, then $f(x)$ ranges from 1 to $\infty$
Therefore,
Range(f) $=(1, \infty) \ldots(6)$
From (4), (5) & (6) the range of f(x) as whole:
Range $(f)=0 \cup(1, \infty)$
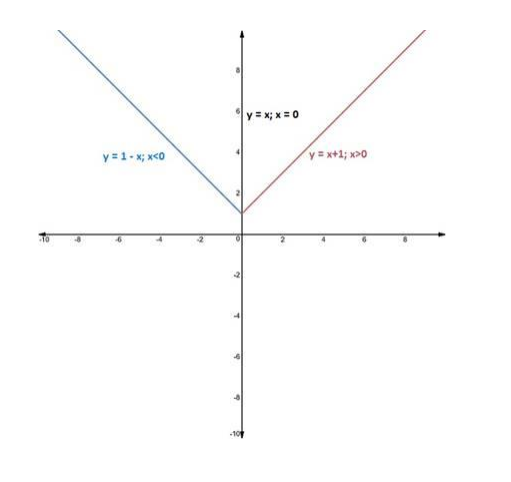
Graph:
