Question:
Consider the quadratic equation
$(c-5) x^{2}-2 c x+(c-4)=0, c \neq 5$. Let $S$ be the set
of all integral values of $\mathrm{c}$ for which one root of the equation lies in the interval $(0,2)$ and its other root lies in the interval $(2,3)$. Then the number of elements in $S$ is :
Correct Option: 1
Solution:
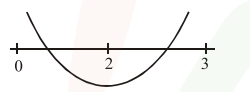
Let $f(x)=(c-5) x^{2}-2 c x+c-4$
$\therefore f(0) f(2)<0$ ...................(1)
$\& f(2) f(3)<0$ ..............(2)
from (1) \& (2)
$(c-4)(c-24)<0$
$\&(c-24)(4 c-49)<0$
$\Rightarrow \frac{49}{4} $\therefore s=\{13,14,15, \ldots .23\}$ Number of elements in set $S=11$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
