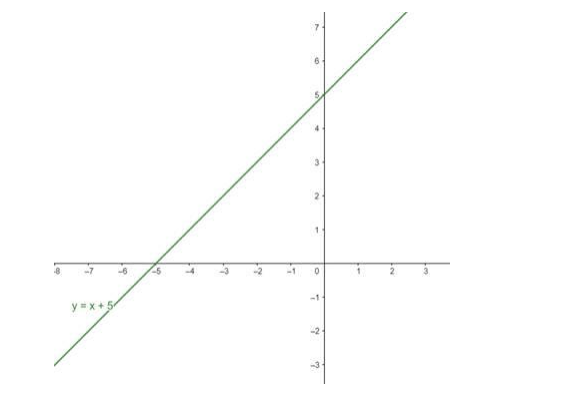
Consider the real function $\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}: \mathrm{f}(\mathrm{x})=\mathrm{x}+5$ for all
$x \in R$. Find its domain and range. Draw the graph of this function.
Given: $f(x)=x+5 \forall x \in R$
To Find: Domain and Range of f(x).
The domain of the given function is all real numbers expect where the expression is undefined. In this case, there is no real number which makes the expression undefined.
As f(x) is a polynomial function, we can have any value of x.
Therefore,
Domain $(f)=(-\infty, \infty)\{x \mid x \in R\}$
Now
Let $y=f(x)$
$y=x+5$
$x=y-5$
The range is set of all valid values of y
Therefore,
Range $(f)=(-\infty, \infty)\{y \mid y \in R\}$
Graph:
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
