Construct a $\triangle \mathrm{ABC}$ in which $\mathrm{AB}=6 \mathrm{~cm}, \angle \mathrm{A}=30^{\circ}$ and $\angle \mathrm{B}=60^{\circ} .$ Construct another $\Delta \mathrm{AB}^{\prime} \mathrm{C}^{\prime}$ similar to $\Delta \mathrm{ABC}$ with base $\mathrm{AB}^{\prime}=8 \mathrm{~cm}$.
Steps of Construction
Step 1. Draw a line segment AB = 6 cm.
Step 2. At A, draw
Step 3. At B, draw
Thus, ∆ABC is the required triangle.
Step 4. Produce AB to B' such that AB' = 8 cm.
Step 5. From B', draw B'C' || BC meeting AX at C'.
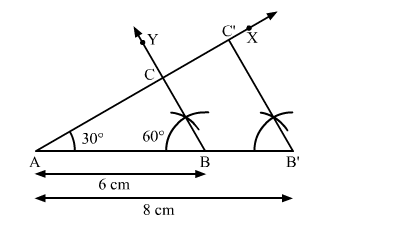
Here, ∆AB'C' is the required triangle similar to ∆ABC.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.