Construct a $\triangle A B C$, in which $B C=5 \mathrm{~cm}, \angle C=60^{\circ}$ and altitude from $A$ is equal to $3 \mathrm{~cm}$. Construct a $\triangle A D E$ similar to $\triangle A B C$, such that each side of $\triangle A D E$ is $\frac{3}{2}$ times the
corresponding side of ∆ABC. Write the steps of construction.
Steps of Construction :
Step 1. Draw a line l .
Step 2. Draw an angle of 90o at M on l .
Step 3. Cut an arc of radius 3 cm on the perpendicular. Mark the point as A.
Step 4. With $\mathrm{A}$ as centre, make an angle of $30^{\circ}$ and let it cut $/$ at $\mathrm{C}$. We get $\angle A C B=60^{\circ}$.
Step 5. Cut an arc of 5 cm from C on l and mark the point as B.
Step 6. Join AB.
Thus, △ABC is obtained .
Step 7 . Extend $A B$ to $D$, such that $B D=\frac{1}{2} B C$.
Step 8. Draw $\mathrm{DE} \| B C$, cutting $\mathrm{AC}$ produced to $\mathrm{E}$.
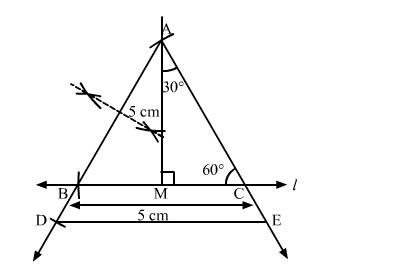
Then, $\triangle \mathrm{ADE}$ is the required triangle, each of whose sides is $\frac{3}{2}$ of the corresponding sides of $\triangle \mathrm{ABC}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
