Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length.

Steps of construction :

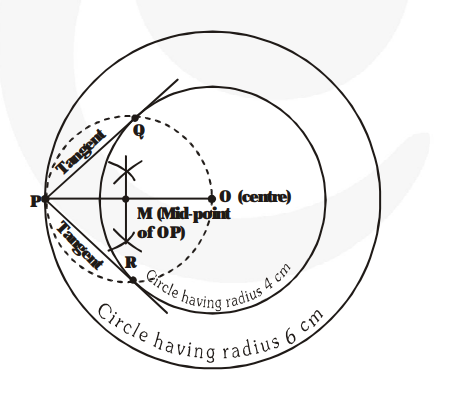
1. Draw two concentric circles having radii 4 cm and 6 cm. O is the centre of the circles.

2. Take any point P on the larger circle.

3. Join OP and mark mid-point M of OP.

4. Taking M as centre and radius = MP = MO, draw circle which intersects the smaller circle in two points Q and R.

5. Join PQ and PR.

Now PQ and PR are the required tangents.

By measurement, we have length of the tangents = 4.4 cm (approx.).

By calculation, we have length of the tangents 

$=\sqrt{\mathbf{O P}^{2}-\mathbf{0 Q}^{2}}=\sqrt{\mathbf{3 B}-\mathbf{1 6}}=\sqrt{\mathbf{2 0}}=\mathbf{2} \sqrt{\mathbf{5}} \mathbf{c m}$