Construct a triangle similar to a given ΔABC such that each of its sides is (2/3)rd

Given that

Construct a triangle of given data, $B C=6 \mathrm{~cm}, \angle \mathrm{B}=50^{\circ}$ and $\angle \mathrm{C}=60^{\circ}$ and then a triangle similar to it whose sides are $(2 / 3)$ of the corresponding sides of $\triangle A B C$.

We follow the following steps to construct the given

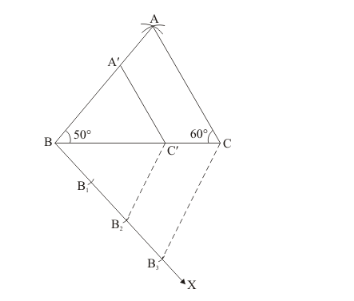
Step of construction

Step: I- First of all we draw a line segment.

Step: II- With B as centre draw an angle.

Step: III- With C as centre draw an anglewhich intersecting the line drawn in step II at A.

Step: IV- Joins $A B$ and $A C$ to obtain $\triangle A B C$.

Step: $V$-Below $B C$, makes an acute angle $\angle C B X=60^{\circ}$.

Step: VI-Along $B X$, mark off three points $B_{1}, B_{2}$ and $B_{3}$ such that $B B_{1}=B_{1} B_{2}=B_{2} B_{3}$

Step: VII -Join $B_{3} C$.

Step: VIII -Since we have to construct a triangle each of whose sides is two-third of the corresponding sides oi $\triangle A B C$.

So, we take two parts out of three equal parts on $B X$ from point $B_{2}$ draw $B_{2} C^{\prime} \| B_{3} C$, and meeting $B C$ at $C^{\prime}$.

Step: IX -From $C^{\prime}$ draw $C^{\prime} A \| A C$, and meeting $A B$ at $A^{\prime}$

Thus, is the required triangle, each of whose sides is two third of the corresponding sides of.