Question.
Construct a triangle $X Y Z$ in which $\angle Y=30^{\circ}, \angle Z=90^{\circ}$ and $X Y+Y Z+Z X=11 \mathrm{~cm}$.
Solution:
The below given steps will be followed to construct the required triangle.
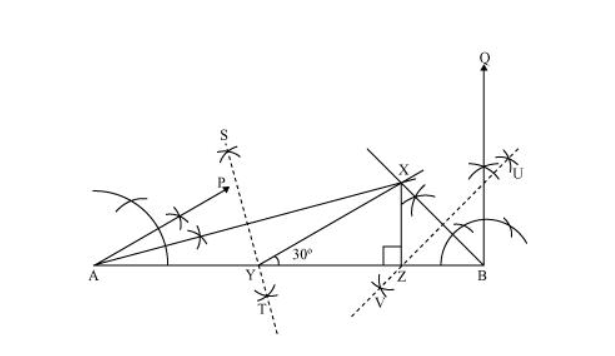
Step I: Draw a line segment AB of 11 cm.
(As $X Y+Y Z+Z X=11 \mathrm{~cm}$ )
Step II: Construct an angle, ∠PAB, of 30° at point A and an angle, ∠QBA, of 90° at point B.
Step III: Bisect ∠PAB and ∠QBA. Let these bisectors intersect each other at point X.
Step IV: Draw perpendicular bisector ST of AX and UV of BX.
Step V: Let ST intersect AB at Y and UV intersect AB at Z.
Join XY, XZ.
$\triangle X Y Z$ is the required triangle.
The below given steps will be followed to construct the required triangle.
Step I: Draw a line segment AB of 11 cm.
(As $X Y+Y Z+Z X=11 \mathrm{~cm}$ )
Step II: Construct an angle, ∠PAB, of 30° at point A and an angle, ∠QBA, of 90° at point B.
Step III: Bisect ∠PAB and ∠QBA. Let these bisectors intersect each other at point X.
Step IV: Draw perpendicular bisector ST of AX and UV of BX.
Step V: Let ST intersect AB at Y and UV intersect AB at Z.
Join XY, XZ.
$\triangle X Y Z$ is the required triangle.

Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
