Question.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
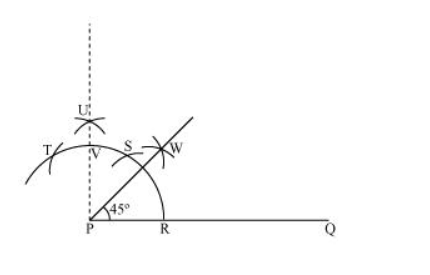
The below given steps will be followed to construct an angle of 45°.
(i) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
(ii) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
(iii) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
(iv) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(v) Join PU. Let it intersect the arc at point V.
(vi) From $R$ and $V$, draw arcs with radius more than $\frac{1}{2} R V$ to intersect each other at $W$. Join $P W$.
PW is the required ray making 45° with PQ.
Justification of Construction:
We can justify the construction, if we can prove $\angle W P Q=45^{\circ}$.
For this, join PS and PT.
We have, $\angle S P Q=\angle T P S=60^{\circ} .$ In (iii) and (iv) steps of this construction, $P U$ was drawn as the bisector of $\angle T P S$.
$\therefore \angle U P S=\frac{1}{2} \angle T P S=\frac{60^{\circ}}{2}=30^{\circ}$
Also, $\angle U P Q=\angle S P Q+\angle U P S$
$=60^{\circ}+30^{\circ}$
$=90^{\circ}$
In step (vi) of this construction, PW was constructed as the bisector of $\angle U P Q$.
$\therefore \angle \mathrm{WPQ}=\frac{1}{2} \angle \mathrm{UPQ}=\frac{90^{\circ}}{2}=45^{\circ}$
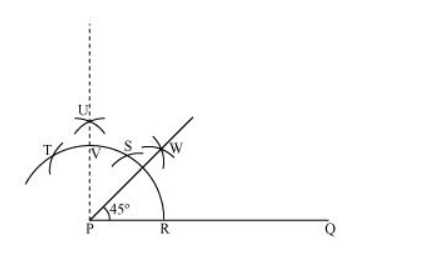
(i) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which intersects PQ at R.
(ii) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
(iii) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
(iv) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(v) Join PU. Let it intersect the arc at point V.
(vi) From $R$ and $V$, draw arcs with radius more than $\frac{1}{2} R V$ to intersect each other at $W$. Join $P W$.
PW is the required ray making 45° with PQ.
Justification of Construction:
We can justify the construction, if we can prove $\angle W P Q=45^{\circ}$.
For this, join PS and PT.
We have, $\angle S P Q=\angle T P S=60^{\circ} .$ In (iii) and (iv) steps of this construction, $P U$ was drawn as the bisector of $\angle T P S$.
$\therefore \angle U P S=\frac{1}{2} \angle T P S=\frac{60^{\circ}}{2}=30^{\circ}$
Also, $\angle U P Q=\angle S P Q+\angle U P S$
$=60^{\circ}+30^{\circ}$
$=90^{\circ}$
In step (vi) of this construction, PW was constructed as the bisector of $\angle U P Q$.
$\therefore \angle \mathrm{WPQ}=\frac{1}{2} \angle \mathrm{UPQ}=\frac{90^{\circ}}{2}=45^{\circ}$