Question.
Construct the angles of the following measurements:
(i) $30^{\circ}$
(ii) $22 \frac{1}{2}$ 。
(iii) $15^{\circ}$
(i) $30^{\circ}$
(ii) $22 \frac{1}{2}$ 。
(iii) $15^{\circ}$
Solution:
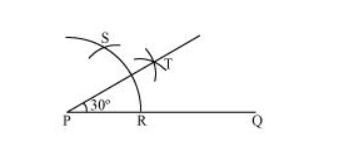
(i) $30^{\circ}$
The below given steps will be followed to construct an angle of 30°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking $R$ and $S$ as centre and with radius more than $\frac{1}{2} R S$, draw arcs to intersect each other at $T$. Join PT which is the required ray making $30^{\circ}$ with the given ray $P Q$.
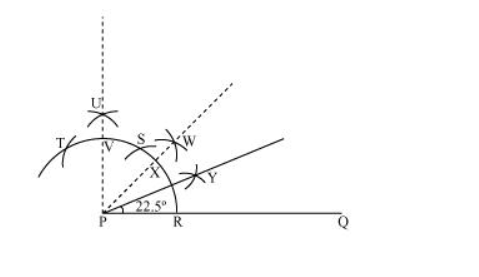
(ii) $22 \frac{1}{2}$ 。
The below given steps will be followed to construct an angle of $22 \frac{1}{2}$.
(1) Take the given ray PQ. Draw an arc of some radius, taking point P as its centre, which intersects PQ at R.
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at point V.
(6) From $R$ and $V$, draw arcs with radius more than $\frac{1}{2} R V$ to intersect each other at $W$. Join $P W$.
(7) Let it intersect the arc at $X$. Taking $X$ and $R$ as centre and radius more than $\frac{1}{2} R X$, draw arcs to intersect each other at $Y$.
Joint PY which is the required ray making $22 \frac{1}{2}^{\circ}$ with the given ray PQ.
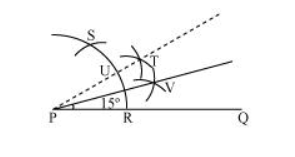
(iii) $15^{\circ}$
The below given steps will be followed to construct an angle of 15°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking $R$ and $S$ as centre and with radius more than $\frac{1}{2} R S$, draw arcs to intersect each other at $T$. Join PT.
Step IV: Let it intersect the arc at $U$. Taking $U$ and $R$ as centre and with radius more than $\frac{1}{2} R U$, draw an arc to intersect each other at $V$. Join $\mathrm{PV}$ which is the required ray making $15^{\circ}$ with the given ray $\mathrm{PQ}$.
(i) $30^{\circ}$
The below given steps will be followed to construct an angle of 30°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking $R$ and $S$ as centre and with radius more than $\frac{1}{2} R S$, draw arcs to intersect each other at $T$. Join PT which is the required ray making $30^{\circ}$ with the given ray $P Q$.
(ii) $22 \frac{1}{2}$ 。
The below given steps will be followed to construct an angle of $22 \frac{1}{2}$.
(1) Take the given ray PQ. Draw an arc of some radius, taking point P as its centre, which intersects PQ at R.
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at point V.
(6) From $R$ and $V$, draw arcs with radius more than $\frac{1}{2} R V$ to intersect each other at $W$. Join $P W$.
(7) Let it intersect the arc at $X$. Taking $X$ and $R$ as centre and radius more than $\frac{1}{2} R X$, draw arcs to intersect each other at $Y$.
Joint PY which is the required ray making $22 \frac{1}{2}^{\circ}$ with the given ray PQ.
(iii) $15^{\circ}$
The below given steps will be followed to construct an angle of 15°.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at point S.
Step III: Taking $R$ and $S$ as centre and with radius more than $\frac{1}{2} R S$, draw arcs to intersect each other at $T$. Join PT.
Step IV: Let it intersect the arc at $U$. Taking $U$ and $R$ as centre and with radius more than $\frac{1}{2} R U$, draw an arc to intersect each other at $V$. Join $\mathrm{PV}$ which is the required ray making $15^{\circ}$ with the given ray $\mathrm{PQ}$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.