Question.
$\mathrm{D}$ and $\mathrm{E}$ are points on the sides $\mathrm{CA}$ and $\mathrm{CB}$ respectively of a triangle $\mathrm{ABC}$ right angled at $\mathrm{C}$. Prove that $\mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2}$.
$\mathrm{D}$ and $\mathrm{E}$ are points on the sides $\mathrm{CA}$ and $\mathrm{CB}$ respectively of a triangle $\mathrm{ABC}$ right angled at $\mathrm{C}$. Prove that $\mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2}$.
Solution:
In right angled $\triangle \mathrm{ACE}$,
$\mathrm{AE}^{2}=\mathrm{CA}^{2}+\mathrm{CE}^{2}$ ...(1)
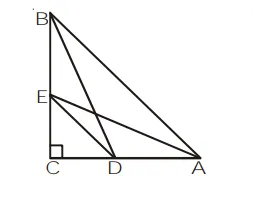
and in right angled $\triangle B C D$,
$\mathrm{BD}^{2}=\mathrm{BC}^{2}+\mathrm{CD}^{2}$ ...(2)
Adding (1) and (2), we get
$\mathrm{AE}^{2}+\mathrm{BD}^{2}=\left(\mathrm{CA}^{2}+\mathrm{CE}^{2}\right)+\left(\mathrm{BC}^{2}+\mathrm{CD}^{2}\right)$
$=\left(\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)+\left(\mathrm{CD}^{2}+\mathrm{CE}^{2}\right)$
$=\mathrm{BA}^{2}+\mathrm{DE}^{2}$
$\therefore \quad \mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2}$
In right angled $\triangle \mathrm{ACE}$,
$\mathrm{AE}^{2}=\mathrm{CA}^{2}+\mathrm{CE}^{2}$ ...(1)
and in right angled $\triangle B C D$,
$\mathrm{BD}^{2}=\mathrm{BC}^{2}+\mathrm{CD}^{2}$ ...(2)
Adding (1) and (2), we get
$\mathrm{AE}^{2}+\mathrm{BD}^{2}=\left(\mathrm{CA}^{2}+\mathrm{CE}^{2}\right)+\left(\mathrm{BC}^{2}+\mathrm{CD}^{2}\right)$
$=\left(\mathrm{BC}^{2}+\mathrm{CA}^{2}\right)+\left(\mathrm{CD}^{2}+\mathrm{CE}^{2}\right)$
$=\mathrm{BA}^{2}+\mathrm{DE}^{2}$
$\therefore \quad \mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.