D and E are the mid-points of the sides AB and AC of ΔABC and 0 is any point on side BC. 0 is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
(a) a square
(b) a rectangle
(c) a rhombus
(d) a parallelogram
Thinking Process
Use the mid-point theorem i.e., the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
(d) In ΔABC, D and E are the mid-points of sides AB and AC, respectively.
By mid-point theorem,
DE || BC …(i)
DE = 1/2 BC
Then, $D E=\frac{1}{2}[B P+P O+O Q+Q C]$
$D E=\frac{1}{2}[2 P O+2 O Q]$
[since, $P$ and $Q$ are the mid-points of $O B$ and $O C$ respectively]
$\Rightarrow \quad D E=P O+O Q$
$\Rightarrow \quad D E=P Q$
Now, in $\triangle A O C, Q$ and $E$ are the mid-points of $O C$ and $A C$ respectively.
[by mid-point theorem]......(iii)
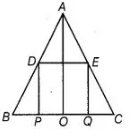
Similarly, in $\triangle A B O, P D \| A O$ and $P D=\frac{1}{2} A O$
[by mid-point theorem].....(iv)
From Eqs. (iii) and (iv),
$E Q \| P D$ and $E Q=P D$
From Eqs. (i) and (ii), $D E \| B C$ (or $D E \| P Q$ ) and $D E=P Q$
Hence, $D E Q P$ is a parallelogram.