D and E are the mid-points of the sides AB and AC, respectively, of ΔABC. DE is produced to F. To prove that CF is equal and parallel to
DA, we need an additional information which is
(a) ∠DAE = ∠EFC
(b) AE = EF
(c) DE = EF
(d) ∠ADE = ∠ECF
(c) in $\triangle A D E$ and $\triangle C F E$, suppose $D E=E F$
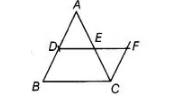
Now. $A E=C E$ [since, $E$ is the mid-point of $A C$ ]
Suppose $D E=E F$
and $\quad \angle A E D=\angle F E C \quad$ [vertically opposite angles]
$\begin{array}{lll}\therefore & \Delta A D E \cong \triangle C F E & \text { [by SAS congruence rule] }\end{array}$
$\begin{array}{lll}\therefore & A D=C F & \text { [by CPCT rule] }\end{array}$
and $\angle A D E=\angle C F E$ [by CPCT]
Hence, $A D \| C F$ [since, alternate interior angles are equal]
Therefore, we need an additional information which is $D E=E F$