Question:
D and E are the points on the sides AB and AC respectively of a ∆ABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm, Prove that BC = 5/2 DE.
Solution:
It is given that $A D=8 \mathrm{~cm}, D B=12 \mathrm{~cm}, A E=6 \mathrm{~cm}$ and $C E=9 \mathrm{~cm}$.
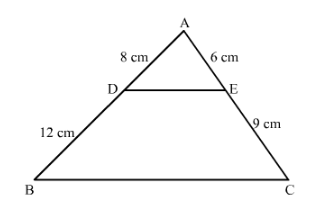
We have to prove that $B C=\frac{5}{2} D E$
Since clearly $\frac{A D}{A B}=\frac{A E}{A C}=\frac{2}{5}$
Also, $\angle A$ is common in $\triangle A B C$ and $\triangle A D E$
So $\triangle A D E \sim \triangle A B C$ (SAS Similarity)
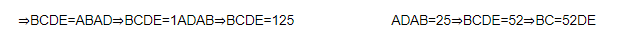
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
