Determine, algebraically, the vertices

Given equation of lines are

3 x – y = 3                                   …………..(i)

2x – 3y = 2                                   ………….(ii)

and x + 2y = 8                                  ………….(iii)

Let lines (i), (ii) and (iii) represent the sides of a ΔABC i.e., AB, BC and CA, respectively. On solving lines (i) and (ii), we will get the intersecting

point B.

On multiplying Eq. (i) by 3 in Eq. (i) and then subtracting, we get

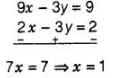
On putting the value of $x$ in Eq. (i), we get

$3 \times 1-y=3$

$\Rightarrow$  $y=0$

So, the coordinate of point or vertex $B$ is $(1,0)$.

Or solving lines (ii) and (iii), we will get the intersecting point $C$.

On multiplying Eq. (iii) by 2 and then subtracting, we get

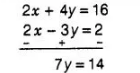
$\Rightarrow \quad y=2$

On putting the value of $y$ in Eq. (iii), we gat

$x+2 \times 2=8$

$\Rightarrow \quad x=8-4$

$\Rightarrow \quad x=4$

Hence, the coordinate of point or vertex $C$ is $(4,2)$.

On solving lines (iii) and (i), we will get the intersecting point $A$.

On multiplying in Eq. (i) by 2 and then adding Eq. (iii), we get

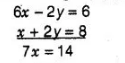
$\Rightarrow \quad x=2$

On putting the value of $x$ in Eq. (i), we get

$3 \times 2-y=3$

$\Rightarrow \quad y=6-3$

$\Rightarrow \quad y=3$

So, the coordinate of point or vertex A is (2, 3).

Hence, the vertices of the ΔABC formed by the given lines are A (2, 3), B (1, 0) and C(4,2).