Determine the mean and standard deviation for the following distribution:

Given the frequency distribution

Now we have to find the mean and standard deviation

Let us make a table of the given data and append other columns after calculations

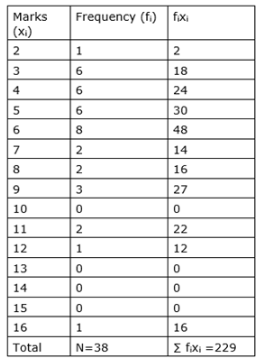
Here mean, $\bar{x}=\frac{\sum f_{\mathrm{f}} \mathrm{x}_{\mathrm{i}}}{\mathrm{N}}=\frac{229}{40}=6.02=6$

So the above table with more columns is as shown below,

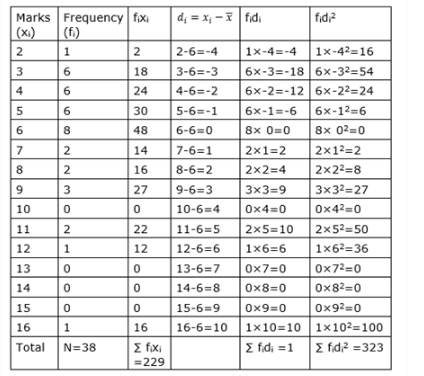
And we know standard deviation is

$\sigma=\sqrt{\frac{\sum f_{i} d_{i}^{2}}{n}-\left(\frac{\sum f_{i} d_{i}}{n}\right)^{2}}$

Substituting values from above table, we get

$\sigma=\sqrt{\frac{323}{38}-\left(\frac{1}{38}\right)^{2}}$

$\sigma=\sqrt{8.5-(0.026)^{2}}$

$\sigma=\sqrt{8.5-0.000676}=\sqrt{8.5}$

$\Rightarrow \sigma=2.9$

Hence the mean and standard deviation of the marks are 6 and $2.9$ respectively.