Diagonals AC and BD of a quadrilateral ABCD intersect at

Solution:



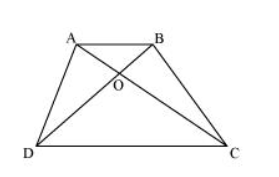
It is given that

Area $(\triangle A O D)=$ Area $(\triangle B O C)$

Area $(\triangle \mathrm{AOD})+$ Area $(\triangle \mathrm{AOB})=$ Area $(\triangle \mathrm{BOC})+$ Area $(\triangle \mathrm{AOB})$

Area $(\triangle \mathrm{ADB})=$ Area $(\triangle \mathrm{ACB})$

We know that triangles on the same base having areas equal to each other lie between the same parallels.

Therefore, these triangles, ΔADB and ΔACB, are lying between the same parallels.

i.e., $A B \| C D$

Therefore, ABCD is a trapezium.