Question.
Diagonals $A C$ and $B D$ of a trapezium $A B C D$ with $A B \| D C$ intersect each other at $O$. Prove that $\operatorname{ar}(A O D)=\operatorname{ar}(B O C)$.
Solution:
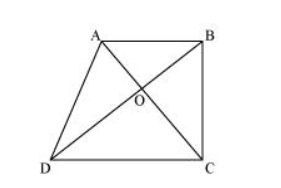
It can be observed that ΔDAC and ΔDBC lie on the same base DC and between the same parallels AB and CD.
$\therefore$ Area $(\Delta \mathrm{DAC})=$ Area $(\Delta \mathrm{DBC})$
$\Rightarrow$ Area $(\Delta D A C)-$ Area $(\Delta D O C)=$ Area $(\Delta D B C)-$ Area $(\Delta D O C)$
$\Rightarrow$ Area $(\triangle A O D)=$ Area $(\triangle B O C)$

It can be observed that ΔDAC and ΔDBC lie on the same base DC and between the same parallels AB and CD.
$\therefore$ Area $(\Delta \mathrm{DAC})=$ Area $(\Delta \mathrm{DBC})$
$\Rightarrow$ Area $(\Delta D A C)-$ Area $(\Delta D O C)=$ Area $(\Delta D B C)-$ Area $(\Delta D O C)$
$\Rightarrow$ Area $(\triangle A O D)=$ Area $(\triangle B O C)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
