Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O.

It is given that trapezium $A B C D$ with $A B \| D C . O$ is the point of intersection of $A C$ and $B D$.

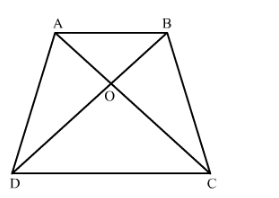
We have to prove that $\frac{O A}{O C}=\frac{O B}{O D}$

Now, in $\triangle A O B$ and $\triangle C O D$

$\angle A O B=\angle C O D \quad$ (Vertically opposite angles)

$\angle \mathrm{OAB}=\angle \mathrm{OCD}$ (Alternate angles)

$\therefore \triangle A O B \sim \triangle C O D \quad$ (AASimilarity)

Hence, $\frac{O A}{O C}=\frac{O B}{O D}$ (Corresponding sides are proportional)