Diagonals of a trapezium PQRS intersect

Given PQRS is a trapezium in which PQ || PS and PQ = 3 RS

$\Rightarrow$ $\frac{P Q}{R S}=\frac{3}{1}$ ...(i)

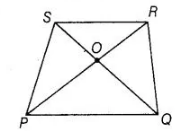
In $\triangle P O Q$ and $\triangle R O S$, $\angle S O R=\angle Q O P$ [vertically opposite angles]

$\angle S R P=\angle R P Q$ [alternate angles]

$\therefore \quad \Delta P O Q \sim \Delta R O S \quad$ [by AAA similarity criterion]

Bv property of area of similar triangle, 

$\frac{\operatorname{ar}(\Delta P O Q)}{\operatorname{ar}(\Delta S O R)}=\frac{(P Q)^{2}}{(R S)^{2}}=\left(\frac{P Q}{R S}\right)^{2}=\left(\frac{3}{1}\right)^{2}$ [from Eq. (i)]

$\Rightarrow$ $\frac{\operatorname{ar}(\Delta P O Q)}{\operatorname{ar}(\Delta S O R)}=\frac{9}{1}$

Hence, the required ratio is 9 :1.