Differentiate the following functions with respect to x :

Let $y=x^{x^{2}-3}+(x-3)^{x^{2}}$

$\Rightarrow y=a+b$

where $a=x^{x^{2}-3} ; b=(x-3)^{x^{2}}$

$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{da}}{\mathrm{dx}}+\frac{\mathrm{db}}{\mathrm{dx}}$

$\left\{\right.$ Using chain rule, $\frac{d(u+a)}{d x}=\frac{d u}{d x}+\frac{d a}{d x}$ where a and $u$ are any variables $\}$

$a=x^{x^{2}-3}$

Taking log both the sides:

$\Rightarrow \log a=\log x^{x^{2}-3}$

$\Rightarrow \log a=\left(x^{2}-3\right) \log x$

$\left\{\log x^{a}=a \log x\right\}$

Differentiating with respect to $x$ :

$\Rightarrow \frac{\mathrm{d}(\log \mathrm{a})}{\mathrm{dx}}=\frac{\mathrm{d}\left(\left(\mathrm{x}^{2}-3\right) \log \mathrm{x}\right)}{\mathrm{dx}}$

$\Rightarrow \frac{\mathrm{d}(\log \mathrm{a})}{\mathrm{dx}}=\left(\mathrm{x}^{2}-3\right) \times \frac{\mathrm{d}(\log \mathrm{x})}{\mathrm{dx}}+\log \mathrm{x} \times \frac{\mathrm{d}\left(\mathrm{x}^{2}-3\right)}{\mathrm{dx}}$

$\left\{\right.$ Using product rule, $\left.\frac{\mathrm{d}(\mathrm{uv})}{\mathrm{dx}}=\mathrm{u} \frac{\mathrm{dv}}{\mathrm{dx}}+\mathrm{v} \frac{\mathrm{du}}{\mathrm{dx}}\right\}$

$\Rightarrow \frac{1}{\mathrm{a}} \frac{\mathrm{da}}{\mathrm{dx}}=\left(\mathrm{x}^{2}-3\right) \times \frac{1}{\mathrm{x}} \frac{\mathrm{dx}}{\mathrm{dx}}+\log \mathrm{x} \times(2 \mathrm{x})$

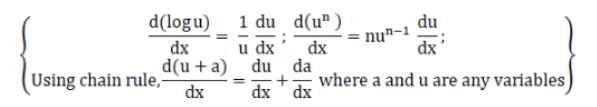
$\Rightarrow \frac{1}{a} \frac{d a}{d x}=\frac{\left(x^{2}-3\right)}{x}+2 x \log x$

$\Rightarrow \frac{d a}{d x}=a\left\{\frac{\left(x^{2}-3\right)}{x}+2 x \log x\right\}$

Put the value of $a=x^{x^{2}-3}:$

$\Rightarrow \frac{d a}{d x}=x^{x^{2}-3}\left\{\frac{\left(x^{2}-3\right)}{x}+2 x \log x\right\}$

$b=(x-3)^{x^{2}}$

Taking log both the sides:

$\Rightarrow \log b=(x-3)^{x^{2}}$

$\Rightarrow \log b=x^{2} \log (x-3)\left\{\log x^{a}=a \log x\right\}$

Differentiating with respect to $\mathrm{x}$ :

$\Rightarrow \frac{d(\log b)}{d x}=\frac{d\left(x^{2} \log (x-3)\right)}{d x}$

$\Rightarrow \frac{d(\log b)}{d x}=x^{2} \times \frac{d(\log (x-3))}{d x}+\log (x-3) \times \frac{d\left(x^{2}\right)}{d x}$

$\left\{\right.$ Using product rule, $\left.\frac{\mathrm{d}(\mathrm{uv})}{\mathrm{dx}}=\mathrm{u} \frac{\mathrm{dv}}{\mathrm{dx}}+\mathrm{v} \frac{\mathrm{du}}{\mathrm{dx}}\right\}$

$\Rightarrow \frac{1}{b} \frac{d b}{d x}=x^{2} \times \frac{1}{(x-3)} \frac{d(x-3)}{d x}+\log (x-3) \times(2 x)$

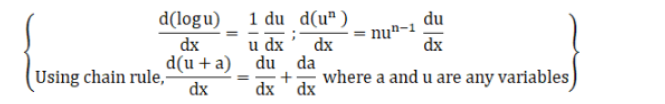
$\Rightarrow \frac{1}{\mathrm{~b}} \frac{\mathrm{db}}{\mathrm{dx}}=\frac{\mathrm{x}^{2}}{(\mathrm{x}-3)}\left(\frac{\mathrm{dx}}{\mathrm{dx}}-\frac{\mathrm{d}(3)}{\mathrm{dx}}\right)+2 \mathrm{x} \log (\mathrm{x}-3)$

$\Rightarrow \frac{1}{\mathrm{~b}} \frac{\mathrm{db}}{\mathrm{dx}}=\frac{\mathrm{x}^{2}}{(\mathrm{x}-3)}(1)+2 \mathrm{x} \log (\mathrm{x}-3)$

$\Rightarrow \frac{\mathrm{db}}{\mathrm{dx}}=\mathrm{b}\left\{\frac{\mathrm{x}^{2}}{(\mathrm{x}-3)}+2 \mathrm{x} \log (\mathrm{x}-3)\right\}$

Put the value of $b=(x-3)^{x^{2}}$ :

$\Rightarrow \frac{\mathrm{db}}{\mathrm{dx}}=(\mathrm{x}-3)^{\mathrm{x}^{2}}\left\{\frac{\mathrm{x}^{2}}{(\mathrm{x}-3)}+2 \mathrm{x} \log (\mathrm{x}-3)\right\}$

$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{da}}{\mathrm{dx}}+\frac{\mathrm{db}}{\mathrm{dx}}$

$\Rightarrow \frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{x}^{\mathrm{x}^{2}-3}\left\{\frac{\left(\mathrm{x}^{2}-3\right)}{\mathrm{x}}+2 \mathrm{x} \log \mathrm{x}\right\}+(\mathrm{x}-3)^{\mathrm{x}^{2}}\left\{\frac{\mathrm{x}^{2}}{(\mathrm{x}-3)}+2 \mathrm{x} \log (\mathrm{x}-3)\right\}$