Solution:
Yes.
According to Euclid’s 5th postulate, when n line falls on l and m and if
$\angle \mathrm{l}+\angle 2<180^{\circ}$, then $\angle 3+\angle 4>180^{\circ}$, producing line $/$ and $m$ further will meet in the side of $\angle 1$ and $\angle 2$ which is less than $180^{\circ}$.
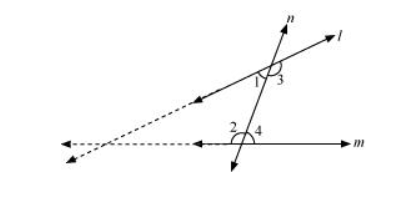
If $\angle \mathrm{l}+\angle 2=180^{\circ}$, then $\angle 3+\angle 4=180^{\circ}$
The lines / and $m$ neither meet at the side of $\angle 1$ and $\angle 2$ nor at the side of $\angle 3$ and $\angle 4$. This means that the lines $/$ and $m$ will never intersect each other. Therefore, it can be said that the lines are parallel.
Yes.
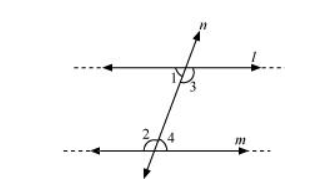
According to Euclid’s 5th postulate, when n line falls on l and m and if
$\angle \mathrm{l}+\angle 2<180^{\circ}$, then $\angle 3+\angle 4>180^{\circ}$, producing line $/$ and $m$ further will meet in the side of $\angle 1$ and $\angle 2$ which is less than $180^{\circ}$.

If $\angle \mathrm{l}+\angle 2=180^{\circ}$, then $\angle 3+\angle 4=180^{\circ}$

The lines / and $m$ neither meet at the side of $\angle 1$ and $\angle 2$ nor at the side of $\angle 3$ and $\angle 4$. This means that the lines $/$ and $m$ will never intersect each other. Therefore, it can be said that the lines are parallel.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
