Does there exist a function which is continuos everywhere but not differentiable at exactly two points? Justify your answer ?
Question:
Does there exist a function which is continuos everywhere but not differentiable at exactly two points? Justify your answer ?
Solution:
$y=\left\{\begin{array}{lc}|x| & -\infty It can be seen from the above graph that, the given function is continuos everywhere but not differentiable at exactly two points which are 0 and 1.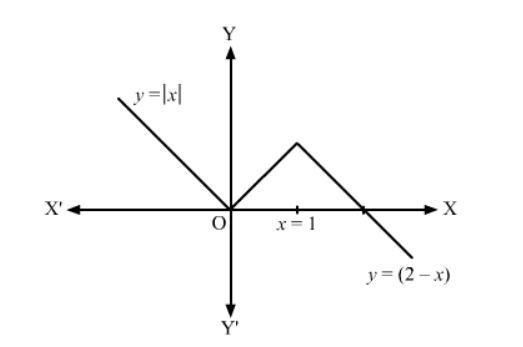
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
