Draw a circle of radius 3 cm. Take two points P and Q on one of its extended

Given that

Construct a circle of radius, and extended diameter each at distance of 7cm from its centre. Construct the pair of tangents to the circle from these two points  .

We follow the following steps to construct the given

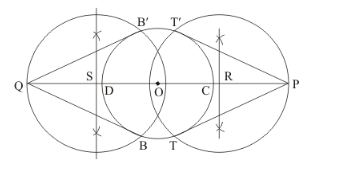
Step of construction

Step: I- First of all we draw a circle of radius $=3 \mathrm{~cm}$.

Step: II- Make a line $C D=$ diameter $-6 \mathrm{~cm}$.

Step: III-Extend the line $C D$ in such a way that point $C P=D Q=7 \mathrm{~cm}$

Step: IV-CP at a distance of $O P=7+3=10 \mathrm{~cm}$, and join $O P$ draw a right bisector of $O P$, intersecting $O P$ at $R$.

Step V:- Similarly, $D Q$ at a distance of $O Q=7+3=10 \mathrm{~cm}$, and join $O Q$ draw a right bisector of $O Q$, intersecting $O Q$ at $S$.

Step VI: Taking R and S as centre and radius $O S=O R$, draw a circle to intersect the given circle at $T$ and $T$ '

B and B ’respectively.

Step: VII- Joins PT and PT’ as well as QB and QB’ to obtain the require tangents.

Thus, are the required tangents.