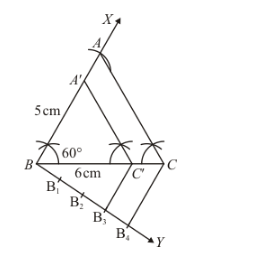
Draw a triangle $A B C$ with side $B C=6 \mathrm{~cm}, A B=5 \mathrm{~cm}$ and $\angle A B C=60^{\circ}$. Then construct a triangle whose sides are $\frac{3}{4}$ time the corresponding sides of $\triangle A B C$.
We have to draw a triangle $A B C$ with $B C=6 \mathrm{~cm}, A B=5 \mathrm{~cm}, \angle A B C=60^{\circ}$
Then we have to construct a similar triangle with side $\frac{3}{4}$ of $\triangle A B C$
Steps of construction
1. Draw a line segment 
2. At B draw 
so that a ray BX is made
3. Keep compass at B and mark an arc of 5 cm at ray BX and name that point as A
4. Join $A C$ to make $\triangle A B C$
5. Draw a ray $\overrightarrow{\mathrm{BY}}$ making an acute angle with $\mathrm{BC}$.
6. Mark 4 points, $B_{1}, B_{2}, B_{3}$, and $B_{4}$ along $B Y$ such that $B B_{1}=B_{1} B_{2}=B_{2} B_{3}=B_{3} B_{4}$.
7. Join CB4
8. Through the point B3, draw a line parallel to B4C by making an angle equal to ∠BB4C, intersecting BC at C′.
9. Through the point C′, draw a line parallel to AC, intersecting BA at A′.
Thus, ΔA′BC′ is the required triangle.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.