Draw a triangle $\mathrm{ABC}$ with side $\mathrm{BC}=7 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ}, \angle \mathrm{A}=105^{\circ} .$ Then construct a triangle whose sides are $\frac{4}{3}$ times the corresponding sides of $\triangle \mathrm{ABC}$.
Steps of construction :
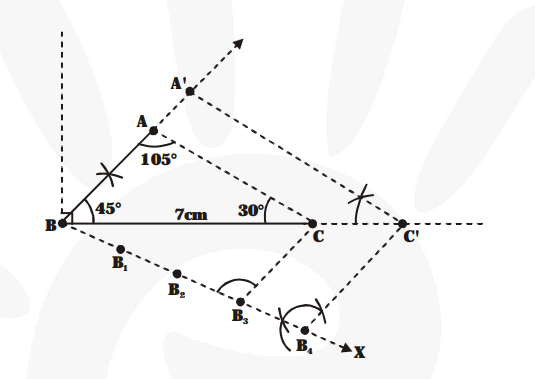
1. Construction $\triangle \mathrm{ABC}$ such that $\mathrm{BC}=7 \mathrm{~cm}$,
$\angle \mathrm{ABC}=45^{\circ}$ and $\angle \mathrm{ACB}=30^{\circ}$ (i.e., $\angle \mathrm{BAC}=105^{\circ}$ ).
2. Draw any ray BX making an acute angle with BC.
3. Take points $\mathrm{B}_{1}, \mathrm{~B}_{2}, \mathrm{~B}_{3}, \mathrm{~B}_{4}$ on $\mathrm{BX}$ such that
$\mathrm{BB}_{1}=\mathrm{B}_{1} \mathrm{~B}_{2}, \mathrm{~B}_{2} \mathrm{~B}_{3}=\mathrm{B}_{3} \mathrm{~B}_{4}$
4. Join $\mathrm{B}_{3} \mathrm{C}$.
5. Through $\mathrm{B}_{4}$ draw $\mathrm{B}_{4} \mathrm{C}^{\prime} \mid \mathrm{B}_{3} \mathrm{C}$ and let it intersect $\mathrm{BC}$ (produced) at $\mathrm{C}^{\prime}$.
6. Through $\mathrm{C}^{\prime}$ draw, $\mathrm{C}^{\prime} \mathrm{A}^{\prime} \| \mathrm{CA}$ and let it intersect $\mathrm{BA}$ (produced) at $\mathrm{A}^{\prime}$.
Now, $\triangle \mathrm{A}^{\prime} \mathrm{BC}^{\prime}$ is the required triangle whose sides are $\frac{4}{3}$ times the corresponding sides of the $\Delta \mathrm{ABC}$.
