Draw an isosceles triangle ABC in

Solution:

Let $\triangle \mathrm{PQR}$ and $\triangle \mathrm{ABC}$ are similar triangles, then its scale factor between the corresponding sides is

$\frac{P Q}{A B}=\frac{8}{6}=\frac{4}{3}$

Steps of construction

1. 1. Draw a line segment BC = 5 cm.
   2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P’.
   3. Taking B and C as centres draw two arcs of equal radius 6 cm intersecting each other at A
   4. Join BA and CA. So, ΔABC is the required isosceles triangle.

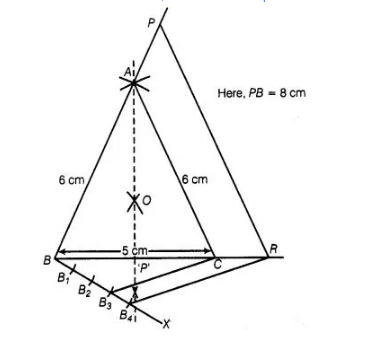
5. From $B$, draw any ray $B X$ making an acute $\angle C B X$

6. Locate four points $B_{1}, B_{2}, B_{3}$ and $B_{4}$ on $B X$ such that $B B_{1}=B_{1} B_{2}=B_{2} B_{3}=B_{3} B_{4}$

7. Join $B_{3} C$ and from $B_{4}$ draw a line $B_{4} R \| B_{3} C$ intersecting the extended line segment $B C$ at $R$.

8. From point R, draw RP\|CA meeting BA produced at P

Then, $\triangle P B R$ is the required triangle.

Justification

$\because \quad \quad B_{4} R \| B_{3} C \quad$ (by construction)

$\therefore$ $\frac{B C}{C R}=\frac{3}{1}$

Now, $\frac{B R}{B C}=\frac{B C+C R}{B C}$

$=1+\frac{C R}{B C}=1+\frac{1}{3}=\frac{4}{3}$

Also, $R P \| C A$

$\therefore$ $\triangle A B C \sim \triangle P B R$

and $\frac{P B}{A B}=\frac{R P}{C A}=\frac{B R}{B C}=\frac{4}{3}$

Hence, the new triangle is similar to the given triangle whose sides are,$\frac{4}{3}$ times, of the

corresponding sides of the isosceles $\triangle A B C$.