Draw the graph of each of the equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:

(i) We are given, 6x - 3y = 12

We get, y = (6x -12)/3

Now, substituting x = 0 in y = - (6x – 12)/3

we get y = - 4

Substituting x = 2 in y = (- 6x -12)/3, we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

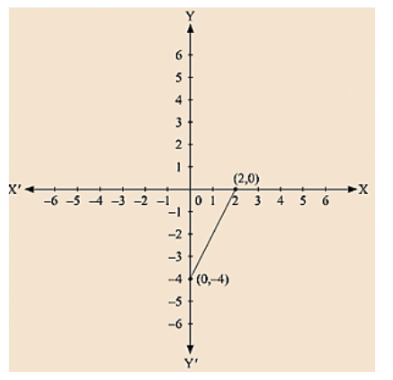
Co-ordinates of the points where graph cuts the co-ordinate axes are y = - 4 at y axis and x = 2 at x axis.

(ii) We are given, - x + 4y = 8

We get, 

$y=\frac{8+x}{4}$

Now, substituting x = 0 in

$y=\frac{8+x}{4}$

we get y = 2

Substituting x = - 8 in

$y=\frac{8+x}{4}$

We get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

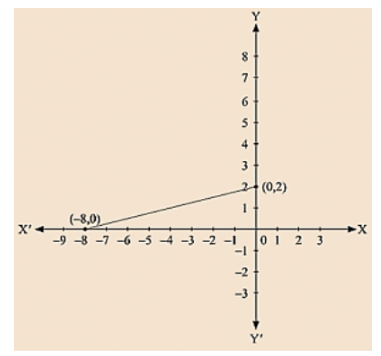
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 2 at y axis and x = -8 at x axis.

(iii) We are given, 2x + y = 6

We get, y = 6 - 2x

Now, substituting x = 0 in y = 6 - 2x we get y = 6

Substituting x = 3 in y = 6 - 2x, we get y = 0  

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

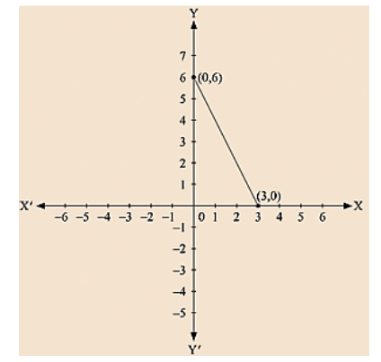
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 6 at y axis and x = 3 at x axis.

(iv) We are given, 3x + 2y + 6 = 0

We get,

$y=\frac{-(6+3 x)}{2}$

Now, substituting x = 0 in

$y=\frac{-(6+3 x)}{2}$

Substituting x = 2 in

$y=\frac{-(6+3 x)}{2}$

we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

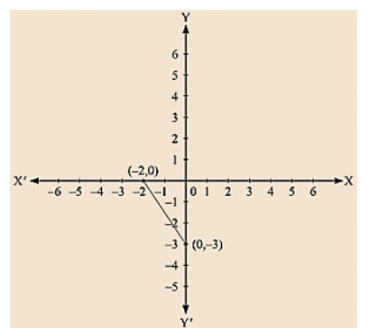
Co-ordinates of the points where graph cuts the co-ordinate axes are y = - 3 at y axis and x = - 2 at x axis.