Draw the graph of each of the following linear equations in two variables:

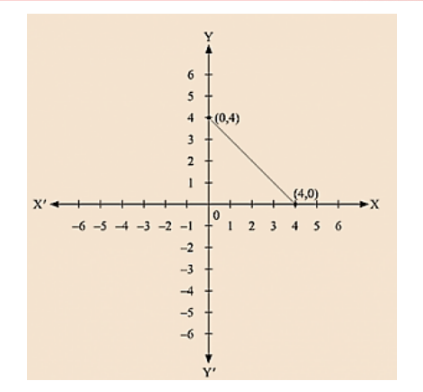
(i) We are given, x + y = 4

We get, y = 4 - x,

Now, substituting x = 0 in y = 4 - x,

We get y = 4

Substituting x = 4 in y = 4 - x, we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given table

(ii) We are given, x - y = 2

We get, y = x – 2

Now, substituting x = 0 in y= x – 2, we get y = - 2

Substituting x = 2 in y = x – 2, we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

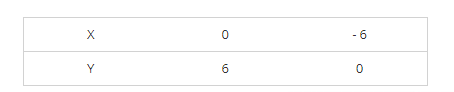
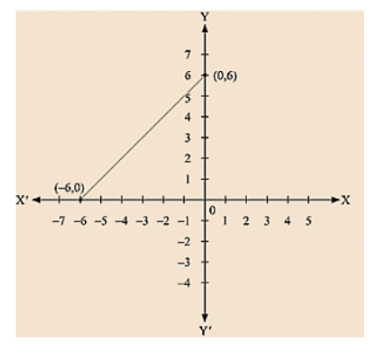
(iii) We are given, - x + y = 6

We get, y = 6 + x

Now, substituting x = 0 in y = 6 + x,

We get y = 6

Substituting x = - 6 in y = 6 + x, we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation.

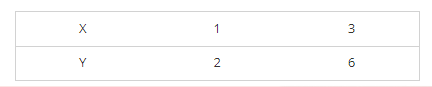
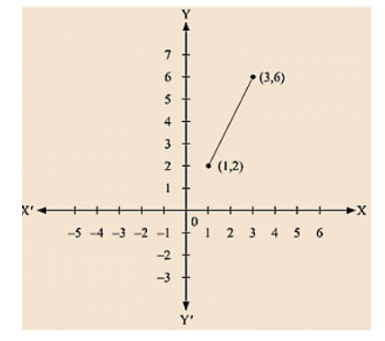
(iv) We are given, y = 2x

Now, substituting x = 1 in y = 2x, we get y = 2

Substituting x = 3 in y = 2x,  we get y = 6

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

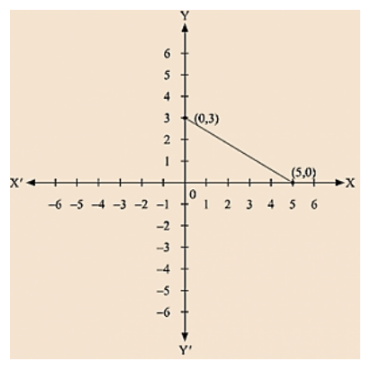
(v) We are given, 3x + 5y = 15

We get, 15 - 3x = 5y

Now, substituting x = 0 in 5y = 15 - 3x,

We get; 5y = 15 y = 3

Substituting x = 5 in 5y = 15 – 3x we get 5y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

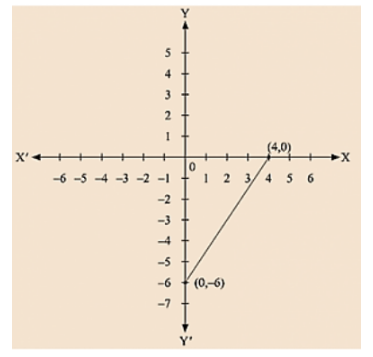
(vi) we are given.

$\frac{x}{2}-\frac{y}{3}=2$

$\frac{3 x-2 y}{6}=2$

3x - 2y = 12 

We get, 

$\frac{3 x-12}{2}=y$

We get y = - 6

Substituting x = 4 in

$\frac{3 x-12}{2}=y$

We get y = 0 Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

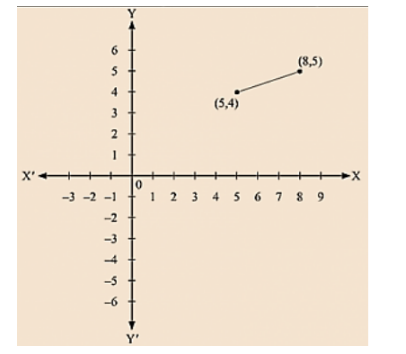
(vii) We are given,

$\frac{x-2}{3}=y-3$

We get, x - 2 = 3(y - 3)

x - 2 = 3y - 9

x = 3y - 7

Now, substituting x = 5 in x = 3y - 7,

We get; y = 4

Substituting x = 8 in x = 3y - 7,

We get; y = 5

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

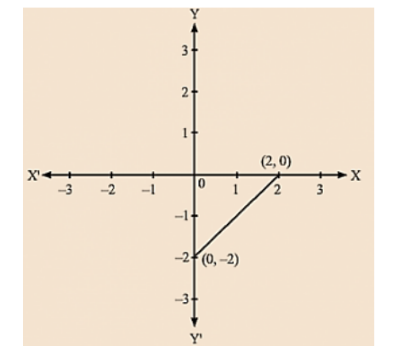
(viii) We are given, 2y = - x +1

We get, 1 – x = 2y

Now, substituting x = 1 in 1– x = 2y, we get y = 0

Substituting x = 5 in 1 – x = 2y, we get y = - 2

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation