Draw the graphs of the linear equations

We are given, 4x - 3y + 4 = 0 

We get,

$y=\frac{4 x+4}{3}$

Now, substituting x = 0 in

$y=\frac{4 x+4}{3}$

we get

Substituting x = -1 in

$y=\frac{4 x+4}{3}$

we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

Plotting E(0, 4/3) and A (-1, 0) on the graph and by joining the points,

We obtain the graph of equation 4x - 3y + 4 = 0.

We are given, 4x + 3y - 20 = 0

We get,

$y=\frac{20-4 x}{3}$

Now, substituting x = 0 in

$y=\frac{20-4 x}{3}$

we get y = 7

Substituting x = 5 in

$y=\frac{20-4 x}{3}$

we get y = 0

Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

Plotting D (0, 20/3) and B (5, 0) on the graph and by joining the points, we obtain the graph of equation 4x +3y - 20 = 0.

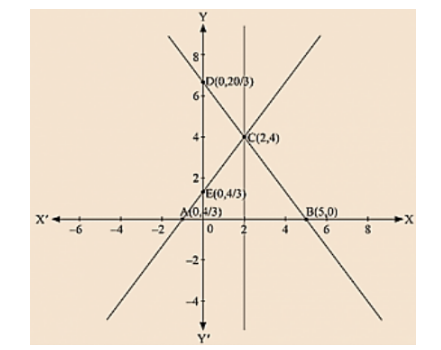
By the intersection of lines formed by 4x - 3y + 4 = 0 and 4x + 3y - 20 = 0 on the graph,

Triangle ABC is formed on x axis.

Therefore, AB at x axis is the base of triangle ABC having AB = 6 units on x axis.

Draw CF perpendicular from C on x axis. CF parallel to y axis is the height of triangle ABC having CF = 4 units on y axis.

Therefore, Area of triangle ABC, say A is given by A = (Base × Height)/2

A = (AB × CF)/2

A = (6 × 4)/2

K = 12 sq. units