Question:
Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a
tangent and verify it by actual calculation.
Solution:
Given, two concentric circles of radii 3 cm and 5 cm with centre 0. We have to draw pair of
tangents from point P on outer circle to the other.
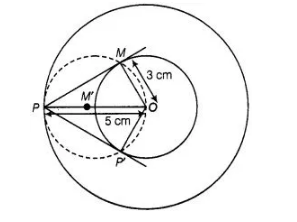
Steps of construction
- Draw two concentric circles with centre 0 and radii 3 cm and 5 cm.
- Taking any point P on outer circle. Join OP.
- Bisect OP, let M’ be the mid-point of .
Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle at M and P’. - Join P M and PP’. Thus, PM and PP’ are the required tangents.
- On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation
In right angle $\triangle O M P$, $\angle P M O=90^{\circ}$
$\therefore$ $P M^{2}=O P^{2}-O M^{2}$
[by Pythagoras theorem i.e. (hypotenuse) $^{2}=(\text { base })^{2}+$ (perpendicular) $^{2}$ ]
$\Rightarrow \quad P M^{2}=(5)^{2}-(3)^{2}=25-9=16$
$\Rightarrow \quad P M=4 \mathrm{~cm}$
Hence, the length of both tangents is $4 \mathrm{~cm}$.