Question.
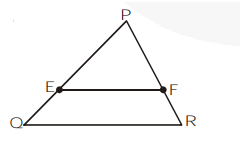
$\mathrm{E}$ and $\mathrm{F}$ are points on the sides $\mathrm{PQ}$ and $\mathrm{PR}$ respectively of a $\Delta \mathrm{PQR}$. For each of the following cases, State whether EF $\| \mathrm{QR}$ :
(i) $\mathrm{PE}=3.9 \mathrm{~cm}, \mathrm{EQ}=3 \mathrm{~cm}, \mathrm{PF}=3.6 \mathrm{~cm}$ and $\mathrm{FR}=2.4 \mathrm{~cm}$.
(ii) $\mathrm{PE}=4 \mathrm{~cm}, \mathrm{QE}=4.5 \mathrm{~cm}, \mathrm{PF}=8 \mathrm{~cm}$ and $\mathrm{RF}=9 \mathrm{~cm}$.
(iii) $\mathrm{PQ}=1.28 \mathrm{~cm}, \mathrm{PR}=2.56 \mathrm{~cm}, \mathrm{PE}=0.18 \mathrm{~cm}$ and $\mathrm{PF}=0.36 \mathrm{~cm}$.
$\mathrm{E}$ and $\mathrm{F}$ are points on the sides $\mathrm{PQ}$ and $\mathrm{PR}$ respectively of a $\Delta \mathrm{PQR}$. For each of the following cases, State whether EF $\| \mathrm{QR}$ :
(i) $\mathrm{PE}=3.9 \mathrm{~cm}, \mathrm{EQ}=3 \mathrm{~cm}, \mathrm{PF}=3.6 \mathrm{~cm}$ and $\mathrm{FR}=2.4 \mathrm{~cm}$.
(ii) $\mathrm{PE}=4 \mathrm{~cm}, \mathrm{QE}=4.5 \mathrm{~cm}, \mathrm{PF}=8 \mathrm{~cm}$ and $\mathrm{RF}=9 \mathrm{~cm}$.
(iii) $\mathrm{PQ}=1.28 \mathrm{~cm}, \mathrm{PR}=2.56 \mathrm{~cm}, \mathrm{PE}=0.18 \mathrm{~cm}$ and $\mathrm{PF}=0.36 \mathrm{~cm}$.
Solution:
(i) In figure
$\frac{P E}{E Q}=\frac{3.9}{3}=1.3$
$\frac{P F}{F R}=\frac{3.6}{2.4}=\frac{3}{2}=1.5$
$\Rightarrow \frac{P E}{E Q} \neq \frac{P F}{F R}$
$\Rightarrow \mathrm{EF}$ is not $\| \mathrm{QR}$
(ii) In figure,
$\frac{P E}{E Q}=\frac{4}{4.5}=\frac{8}{9}$ and $\frac{P F}{F R}=\frac{8}{9}$
$\Rightarrow \frac{P E}{E Q}=\frac{P F}{F R} \Rightarrow E F \| Q R$
(iii) In figure,
$\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{0.18}{\mathrm{PQ}-\mathrm{PE}}=\frac{0.18}{1.28-0.18}=\frac{0.18}{1.10}$
$=\frac{18}{110}=\frac{9}{55}=\frac{P F}{F R}=\frac{0.36}{P R-P F}$
$=\frac{0.36}{2.56-0.36}=\frac{0.36}{2.20}=\frac{9}{55}=\frac{P E}{Q E}=\frac{P F}{F R}$
$\therefore \mathrm{EF} \| \mathrm{QR} \quad$ (By converse of Basic Proportionality Theorem)
(i) In figure
$\frac{P E}{E Q}=\frac{3.9}{3}=1.3$
$\frac{P F}{F R}=\frac{3.6}{2.4}=\frac{3}{2}=1.5$
$\Rightarrow \frac{P E}{E Q} \neq \frac{P F}{F R}$
$\Rightarrow \mathrm{EF}$ is not $\| \mathrm{QR}$
(ii) In figure,
$\frac{P E}{E Q}=\frac{4}{4.5}=\frac{8}{9}$ and $\frac{P F}{F R}=\frac{8}{9}$
$\Rightarrow \frac{P E}{E Q}=\frac{P F}{F R} \Rightarrow E F \| Q R$
(iii) In figure,
$\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{0.18}{\mathrm{PQ}-\mathrm{PE}}=\frac{0.18}{1.28-0.18}=\frac{0.18}{1.10}$
$=\frac{18}{110}=\frac{9}{55}=\frac{P F}{F R}=\frac{0.36}{P R-P F}$
$=\frac{0.36}{2.56-0.36}=\frac{0.36}{2.20}=\frac{9}{55}=\frac{P E}{Q E}=\frac{P F}{F R}$
$\therefore \mathrm{EF} \| \mathrm{QR} \quad$ (By converse of Basic Proportionality Theorem)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.