Evaluate :

To find: Value of $(2+\sqrt{3})^{7}+(2-\sqrt{3})^{7}$

Formula used: (i) ${ }^{n} C_{r}=\frac{n !}{(n-r) !(r) !}$

(ii) $(a+b)^{n}={ }^{n} C_{0} a^{n}+{ }^{n} C_{1} a^{n-1} b+{ }^{n} C_{2} a^{n-2} b^{2}+\ldots \ldots+{ }^{n} C_{n-1} a b^{n-1}+{ }^{n} C_{n} b^{n}$

$\begin{aligned} &\left[{ }^{7} C_{0} a^{7}\right]+\left[{ }^{7} C_{1} a^{7-1} b\right]+\left[{ }^{7} C_{2} a^{7-2} b^{2}\right]+\left[{ }^{7} C_{3} a^{7-3} b^{3}\right]+\left[{ }^{7} C_{4} a^{7-4} b^{4}\right]+\\(a+b)^{7}=&\left[{ }^{7} C_{5} a^{7-5} b^{5}\right]+\left[{ }^{7} C_{6} a^{7-6} b^{6}\right]+\left[{ }^{7} C_{7} b^{7}\right] \end{aligned}$

$\Rightarrow{ }^{7} \mathrm{C} 0 \mathrm{a}^{7}+{ }^{7} \mathrm{C}_{1} \mathrm{a}^{6} \mathrm{~b}+{ }^{7} \mathrm{C} 2 \mathrm{a}^{5} \mathrm{~b}^{2}+{ }^{7} \mathrm{C} 3 \mathrm{a}^{4} \mathrm{~b}^{3}+{ }^{7} \mathrm{C} 4 \mathrm{a}^{3} \mathrm{~b}^{4}+{ }^{7} \mathrm{C} 5 \mathrm{a}^{2} \mathrm{~b}^{5}+{ }^{7} \mathrm{C} 6 \mathrm{a}^{1} \mathrm{~b}^{6}+{ }^{7} \mathrm{C} 7 \mathrm{~b}^{7} \ldots$ (i)

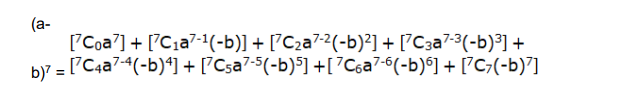
$\Rightarrow{ }^{7} \mathrm{C} 0 \mathrm{a}^{7}-{ }^{7} \mathrm{C} 1 \mathrm{a}^{6} \mathrm{~b}+{ }^{7} \mathrm{C} 2 \mathrm{a}^{5} \mathrm{~b}^{2}-{ }^{7} \mathrm{C} 3 \mathrm{a}^{4} \mathrm{~b}^{3}+{ }^{7} \mathrm{C} 4 \mathrm{a}^{3} \mathrm{~b}^{4}-{ }^{7} \mathrm{C} 5 \mathrm{a}^{2} \mathrm{~b}^{5}+{ }^{7} \mathrm{C} 6 \mathrm{a}^{1} \mathrm{~b}^{6}-{ }^{7} \mathrm{C} 7 \mathrm{~b}^{7} \ldots$ (ii)

Adding eqn. (i) and (ii)

$(a+b)^{7}+(a-b)^{7}=\left[{ }^{7} C_{0} a^{7}+{ }^{7} C_{1} a^{6} b\right.$

$\left.+{ }^{7} C_{2} a^{5} b^{2}+{ }^{7} C_{3} a^{4} b^{3}+{ }^{7} C_{4} a^{3} b^{4}+{ }^{7} C_{5} a^{2} b^{5}+{ }^{7} C_{6} a^{1} b^{6}+{ }^{7} C_{7} b^{7}\right]+\left[{ }^{7} C_{0} a^{7}-{ }^{7} C_{1} a^{6} b\right.$

$\left.+{ }^{7} C_{2} a^{5} b^{2}-{ }^{7} C_{3} a^{4} b^{3}+{ }^{7} C_{4} a^{3} b^{4}-{ }^{7} C_{5} a^{2} b^{5}+{ }^{7} C_{6} a^{1} b^{6}-{ }^{7} C_{7} b^{7}\right]$

$\Rightarrow 2\left[{ }^{7} C_{0} a^{7}+{ }^{7} C_{2} a^{5} b^{2}+{ }^{7} C_{4} a^{3} b^{4}+{ }^{7} C_{6} a^{1} b^{6}\right]$

$\Rightarrow 2\left[\left[\frac{7 !}{o !(7-0) !} a^{7}\right]+\left[\frac{7 !}{2 !(7-2) !} a^{5 b^{2}}\right]+\left[\frac{7 !}{4 !(7-4) !} a^{3} b^{4}\right]+\left[\frac{7 !}{6 !(7-6) !} a^{1} b^{6}\right]\right]$

$\Rightarrow 2\left[(1) a^{7}+(21) a^{5} b^{2}+(35) a^{3} b^{4}+(7) a b^{6}\right]$

$\Rightarrow 2\left[a^{7}+21 a^{5} b^{2}+35 a^{3} b^{4}+7 a b^{6}\right]=(a+b)^{7}+(a-b)^{7}$

Putting the value of $a=2$ and $b=\sqrt{3}$ in the above equation

$(2+\sqrt{3})^{7}+(2-\sqrt{3})^{7}$

$=2\left[\left\{2^{7}\right\}+\left\{21(2)^{5}(\sqrt{3})^{2}\right\}+\left\{35(2)^{3}(\sqrt{3})^{4}\right\}+\left\{7(2)(\sqrt{3})^{6}\right\}\right]$

$=2[128+21(32)(3)+35(8)(9)+7(2)(27)]$

$=2[128+2016+2520+378]$

$=10084$

Ans) 10084