Question:
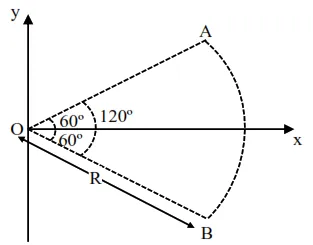
Figure shows a rod $\mathrm{AB}$, which is bent in a $120^{\circ}$ circular arc of radius R. A charge (-Q) is uniformly distributed over rod $\mathrm{AB}$. What is the electric field $\vec{E}$ at the centre of curvature $O$ ?
Correct Option: , 2
Solution:
$\varepsilon=\frac{2 \mathrm{k} \lambda}{\mathrm{R}} \sin \left(\frac{\theta}{2}\right)(-\hat{\mathrm{i}})$
$\lambda=\left(\frac{-Q}{R \theta}\right)=\left(\frac{-Q}{R \cdot \frac{2 \pi}{3}}\right)$
$\lambda=\frac{-3 Q}{2 \pi R}$
$\varepsilon=\frac{2 \mathrm{k}}{\mathrm{R}} \cdot \frac{-3 \mathrm{Q}}{2 \pi \mathrm{R}} \cdot \sin \left(60^{\circ}\right)(-\hat{\mathrm{i}})$
$\varepsilon=\frac{3 \sqrt{3} \mathrm{Q}}{8 \pi^{2} \in_{\mathrm{o}} \mathrm{R}^{2}}(+\hat{\mathrm{i}})$
